Lecture 3D Geometry Processing

Shape Deformation

Prof. Dr. David Bommes

Computer Graphics Group

Shape Deformation

Shape Deformation

Deform face scan through motion tracking

Recap: Fairing

Membrane Surfaces

Minimize surface area \[\int_\set{S} \func{d}A \;\to\; \min \quad\text{with}\quad \delta\set{S}=\bar{\vec{x}}\]
Simpler energy using partial derivatives \[\int_\Omega \norm{\vec{x}_{,u}}^2 + \norm{\vec{x}_{,v}}^2 \func{d}u\func{d}v \;\to\;\min\]
Variational calculus gives \[ \begin{align} \laplace_{\set{S}} \vec{x} &= \vec{0}, & \vec{x} \in \set{S} \setminus \partial\set{S} \\ \vec{x} &= \bar{\vec{x}}, & \vec{x} \in \partial\set{S} \end{align} \]

Thin Plate Surfaces

Minimize surface curvature \[\int_\set{S} \kappa_1^2 + \kappa_2^2 \,\func{d}A \to \min \;\text{with}\; \begin{cases} \delta\set{S}=\bar{\vec{x}} \\ \vec{n}\of{\delta\set{S}}=\bar{\vec{n}} \end{cases}\]

Simpler energy using partial derivatives \[\int_\Omega \norm{\vec{x}_{,uu}}^2 + 2\norm{\vec{x}_{,uv}}^2 + \norm{\vec{x}_{,vv}}^2 \func{d}u\func{d}v \;\to\;\min\]
Variational calculus gives \[\begin{align} \laplace_{\set{S}}^2 \vec{x} &= \vec{0}, & \vec{x} \in \set{S} \setminus \partial\set{S} \\ \vec{x} &= \bar{\vec{x}}, & \vec{x} \in \partial\set{S} \\ \vec{n}\of{\vec{x}} &= \bar{\vec{n}}, & \vec{x} \in \partial\set{S} \\ \end{align}\]

Fairness Functionals

\[\laplace_{\set{S}} \vec{x} = 0\]

\[\laplace_{\set{S}}^2 \vec{x} = 0\]

\[\laplace_{\set{S}}^3 \vec{x} = 0\]

Surface Deformation

Spline Surfaces

Tensor product surfaces
- “Curves of curves”
- Rectangular grid of control points
- Rectangular surface patch

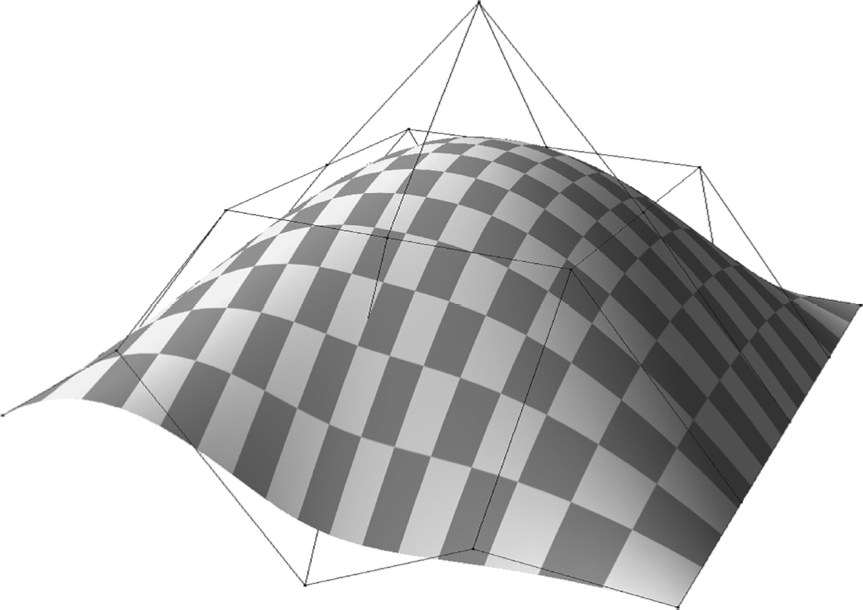
Problems
- Many patches for complex models
- Smoothness across patch boundaries
- Trimming for non-rectangular patches

Subdivision Surfaces

Generalization of spline curves / surfaces
Arbitrary control meshes
Successive mesh refinement with simple rules
Converges to smooth limit surface

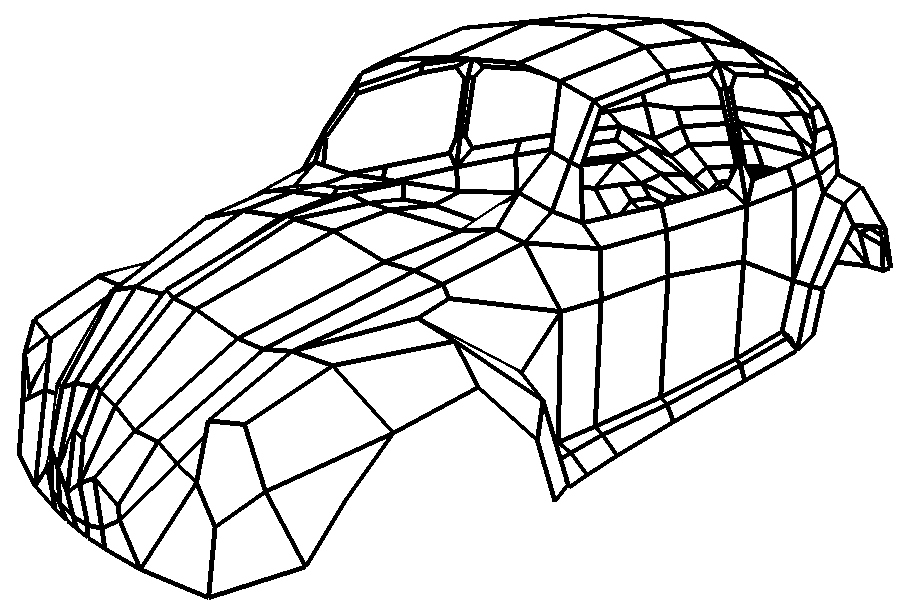
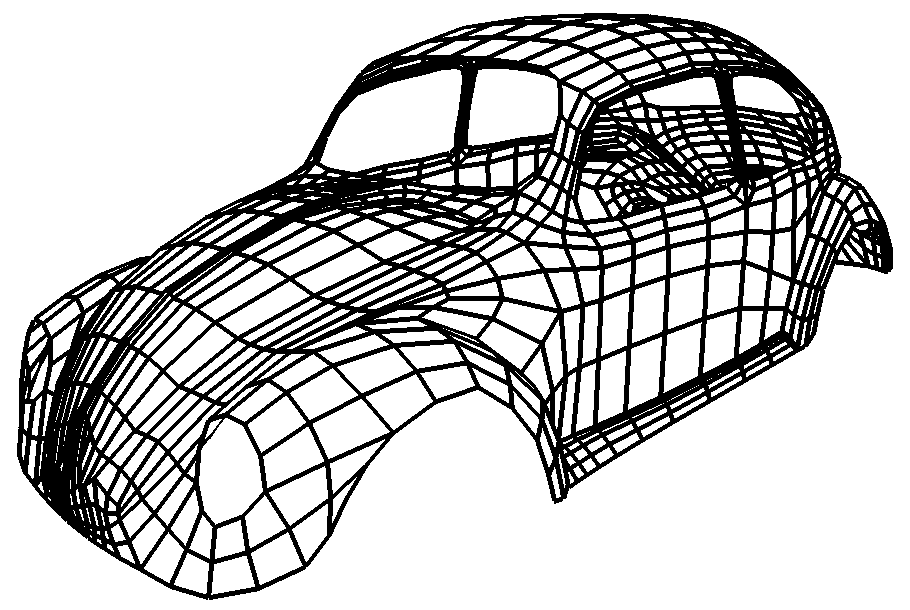
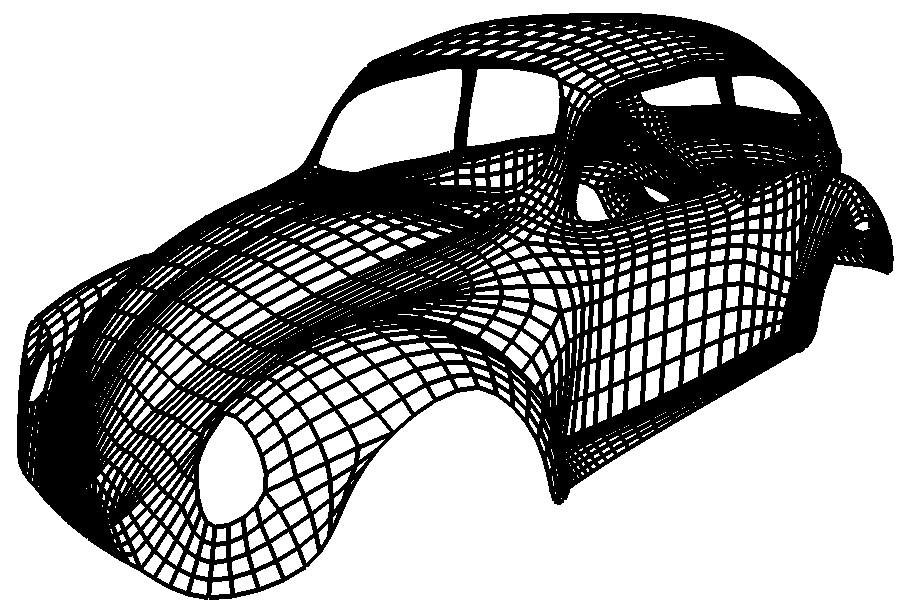
Spline & Subdivision Surfaces

Basis functions are smooth bumps
- Fixed support
- Fixed control grid
Bound to control points
- Initial patch layout is crucial
- Patch design requires experts
Decouple deformation from surface representation!

Modeling Metaphor

Mesh deformation through displacement function \(\vec{d} \colon \set{S} \to \R^3\)
- Fix some vertices (gray)
- Interactively displace handle vertices (yellow)
- Solve for displacement of remaining vertices (blue)

Modeling Metaphor

Mesh deformation through displacement function \(\vec{d} \colon \set{S} \to \R^3\)
- Fix some vertices (gray)
- Interactively displace handle vertices (yellow)
- Solve for displacement of remaining vertices (blue)

\[ \begin{align*} \vec{d} \colon \set{S} &\to \R^3\\ \vec{x}_i &\mapsto \vec{x}_i + \vec{d}\of{\vec{x}_i} \end{align*} \]

Physically-Based Deformation

Nonlinear stretching & bending energies \[ \int_{\Omega} k_s \norm{\mat{I} - \mat{I}'}^2 + k_b \norm{\mat{I\!I} - \mat{I\!I}'}^2 \;\func{d}u\func{d}v \]
Simplified quadratic energy using partial derivatives \[ \int_\Omega k_s \left( \norm{\vec{d}_u}^2+ \norm{\vec{d}_v}^2 \right) \;+\; k_b \left( \norm{\vec{d}_{uu}}^2+ 2\norm{\vec{d}_{uv}}^2+ \norm{\vec{d}_{vv}}^2 \right) \func{d}u \func{d}v \]
Variational calculus gives \[ \begin{align} -k_s \laplace_{\set{S}} \vec{d} \;+\; k_b \laplace_{\set{S}}^2 \vec{d} &\;=\; \vec{0} ,& \text{in blue region} \\ \vec{d} &= \bar{\vec{d}}, & \text{in yellow handle region}\\ \vec{d} &= \vec{0}, & \text{in gray fixed region} \end{align} \]

Deformation Energies

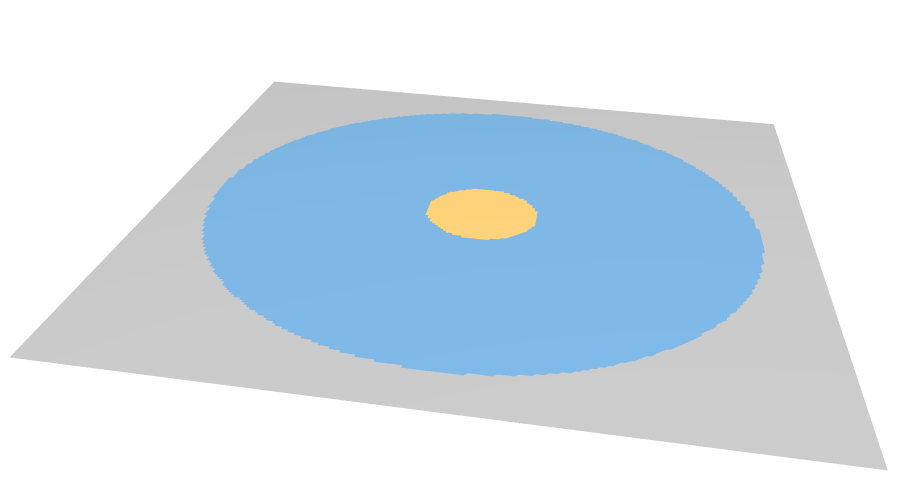
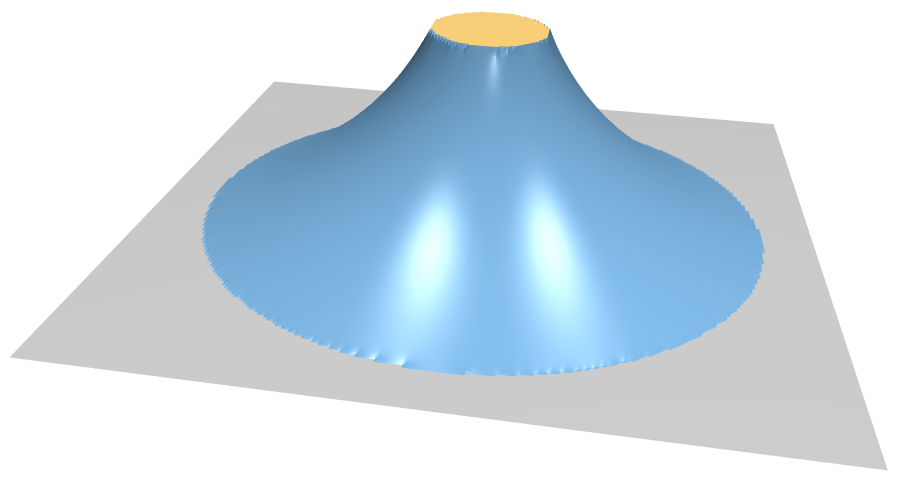
Discretization

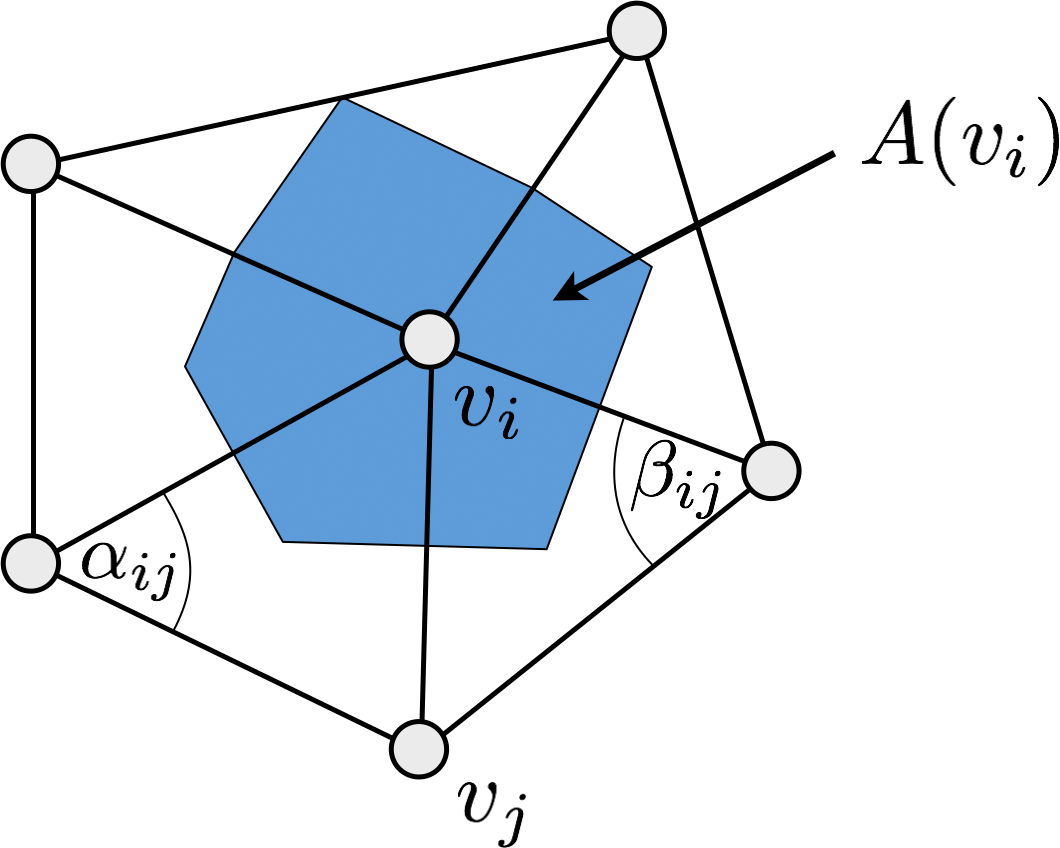
Discretization of Laplace & bi-Laplace
- \[ \begin{align} \laplace \vec{d}_i &= \frac{1}{2A_i} \sum_{j\in\set{N}_i} \left( \cot\alpha_{ij}+\cot\beta_{ij} \right) \left( \vec{d}_j - \vec{d}_i \right) \\[2mm] \laplace^2\vec{d}_i &= \laplace\of{\laplace\vec{d}_i} \end{align} \]

Leads to sparse linear system \[ \matrix{ & \color{blue}{\laplace^2} & \\ \mat{0} & \color{gray}{\mat{I}} & \mat{0} \\ \mat{0} & \mat{0} & \color{green}{\mat{I}} } \matrix{ \vdots \\ \vec{d}_i \\ \vdots } \;=\; \matrix{ \color{blue}{\mat{0}} \\ \color{gray}{\mat{0}} \\ \color{green}{\delta\vec{h}_i} } \]

Car Deformation

Facial Motion Capture

Linear Face Deformation

MoCap markers control facial deformation
Minimize quadratic bending energy by solving linear system

Nonlinear Face Deformation

Add nonlinear wrinkle effects & realistic rendering

Limitations

Problematic cases for surface-based/mesh-based deformations

Space Deformation

Freeform Deformation

Space warp function \(\vec{d} \colon \R^3 \to \R^3\)
- Deform each 3D point: \(\vec{p} \mapsto \vec{d(p)}\)
- Deform each mesh vertex
- Deform control points of freeform curves/surfaces

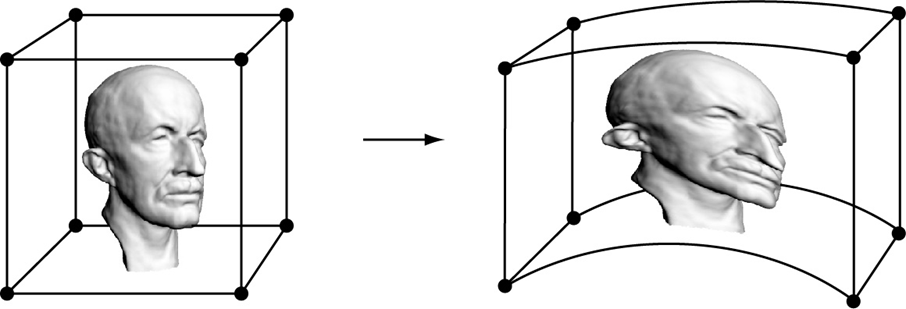
Tensor product Bezier deformation
- \[ \vec{d}(u,v,w) = \sum_{i=0}^l \sum_{j=0}^m \sum_{k=0}^n \vec{b}_{i,j,k} B_i^l(u) B_j^m(v) B_k^n(w) \]

Sederberg & Perry, SIGGRAPH 1986

Freeform Deformation

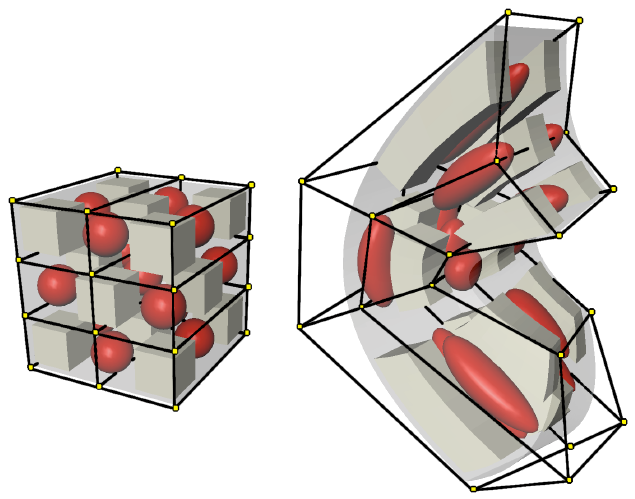
Tensor product spline deformations allow for local control \[ \vec{d}(u,v,w) = \sum_{i=0}^l \sum_{j=0}^m \sum_{k=0}^n \vec{d}_{i,j,k} N_i^l(u) N_j^m(v) N_k^n(w) \]

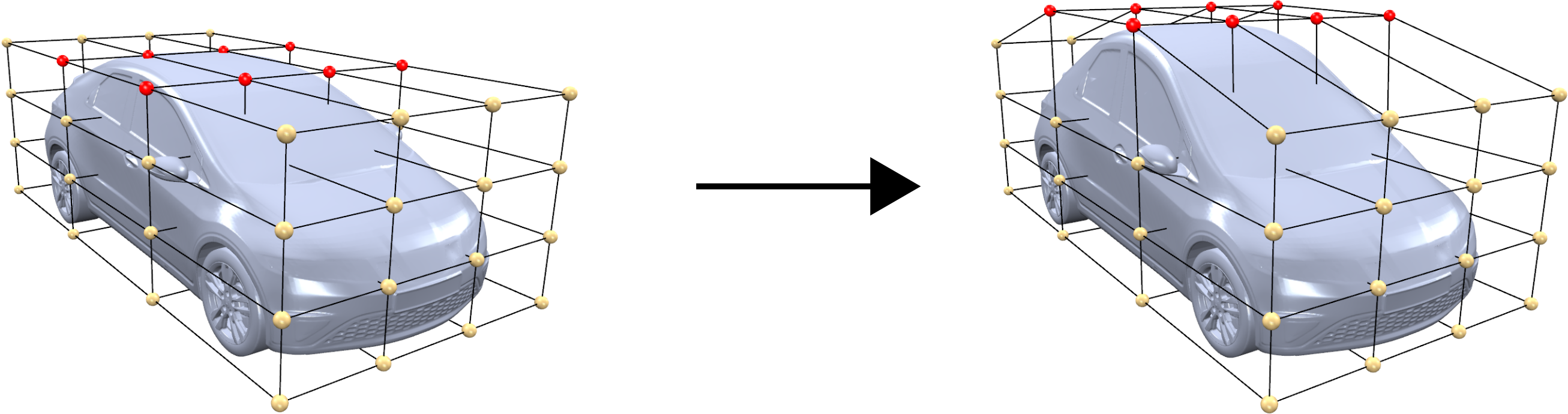
Sederberg & Perry, SIGGRAPH 1986

Spline-Based FFD

Sederberg & Perry, SIGGRAPH 1986

Direct Manipulation FFD

How to prescribe displacement constraints?
- Solve linear system for control points
- Can be over- or under-determined
- Pseudo-inverse: least squares, least norm

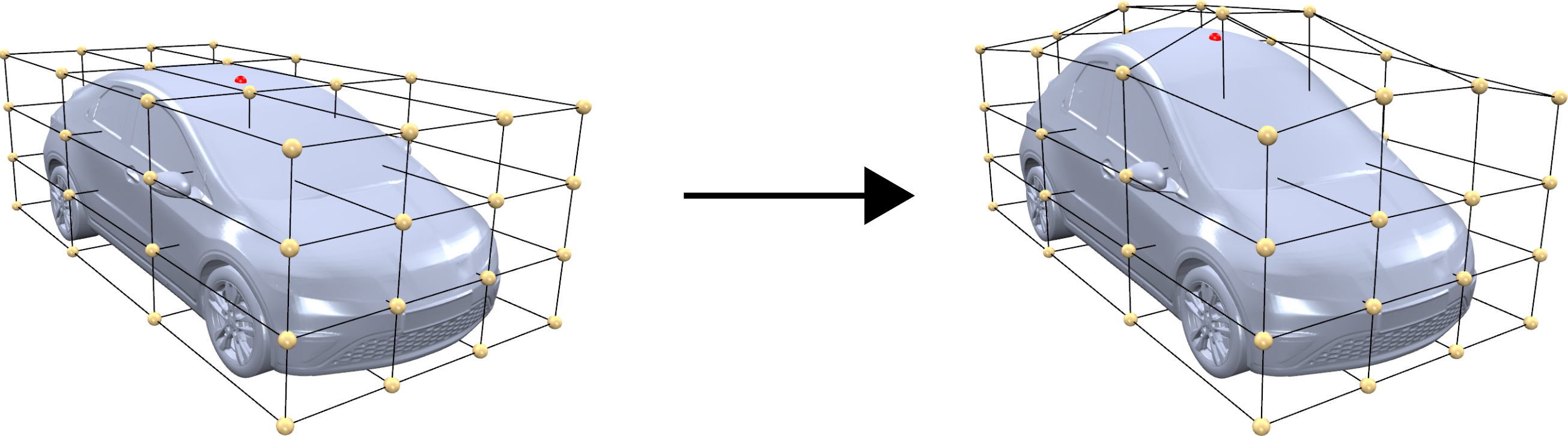
Hsu et al, SIGGRAPH 1992

Direct Manipulation FFD

Hsu et al, SIGGRAPH 1992

Direct Manipulation FFD

Bad: results depends a lot on grid resolution
Minimize control point movement ≠ minimize physical energies!

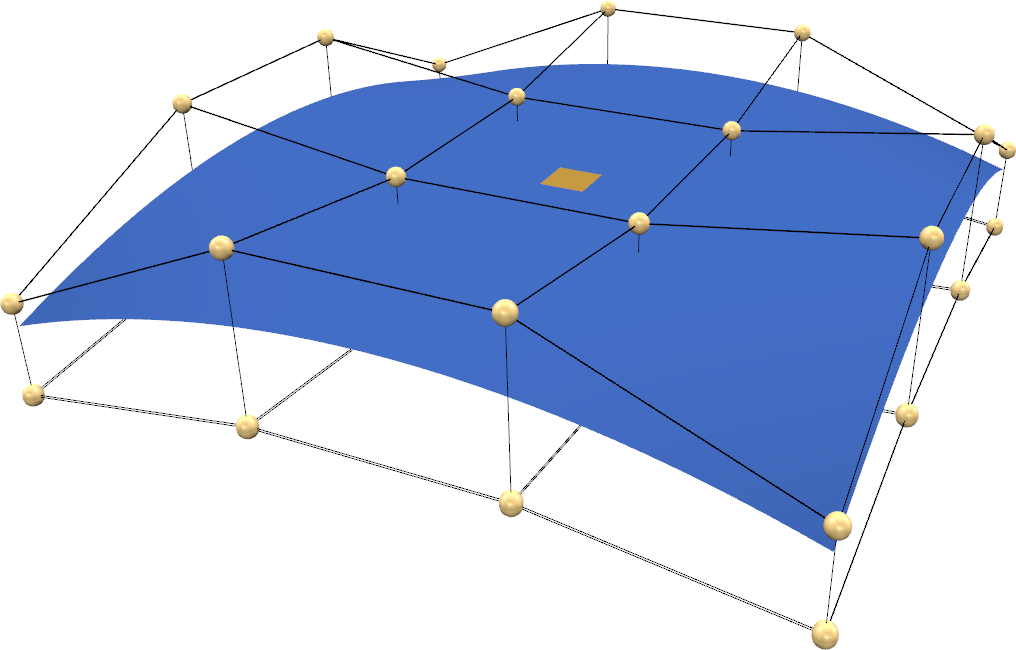
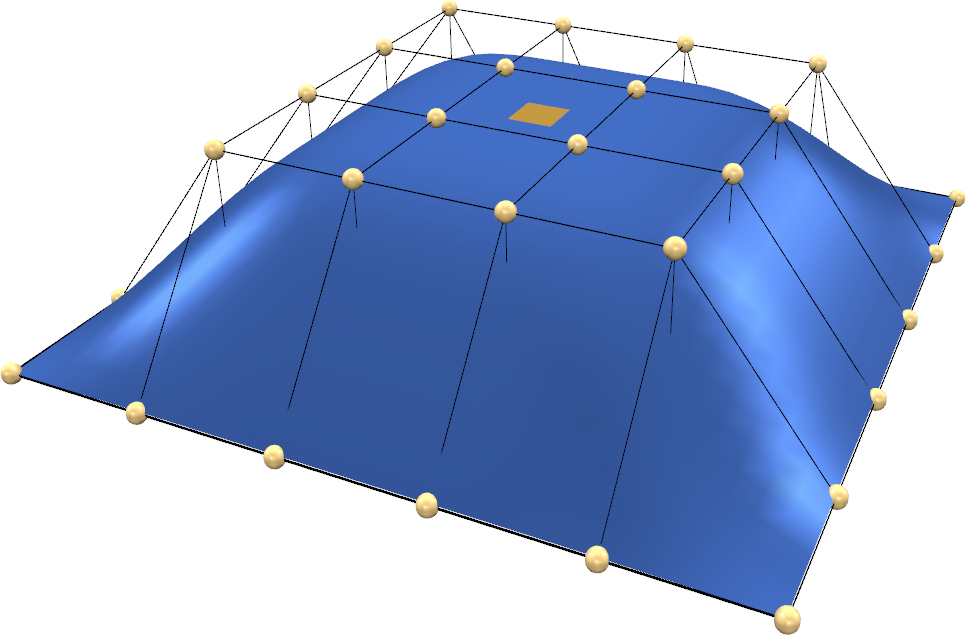
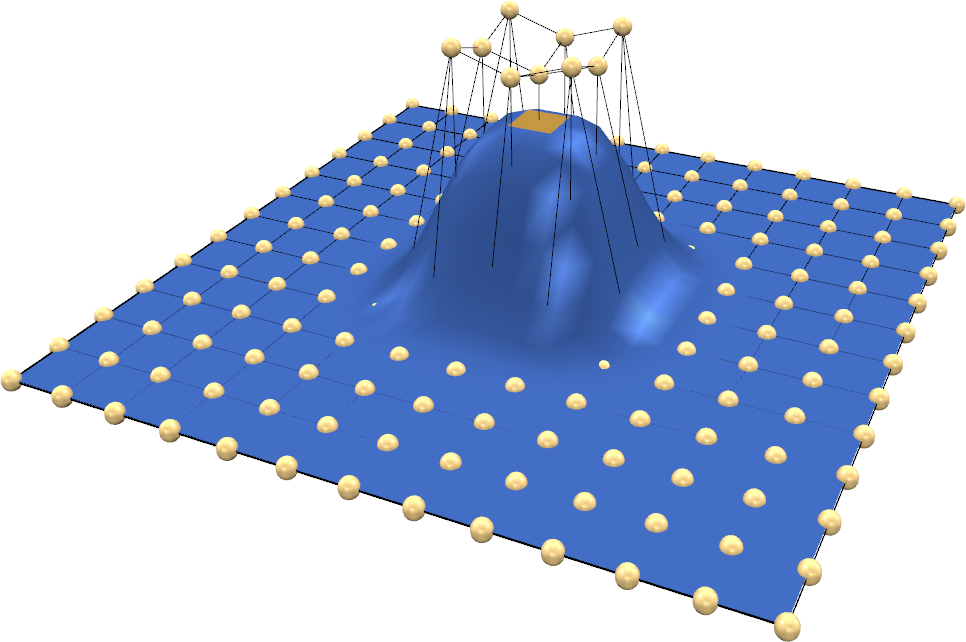
Hsu et al, SIGGRAPH 1992

Modeling Metaphor

Mesh deformation through displacement func. \(\vec{d} \colon \R^3 \to \R^3\)
- Fix some vertices (gray)
- Interactively displace handle vertices (yellow)
- Solve for displacement of remaining vertices (blue)

\[\begin{align*} \vec{d} \colon {\color{red} \R^3} &\to \R^3\\ \vec{x}_i &\mapsto \vec{x} + \vec{d}\of{\vec{x}_i} \end{align*}\]

Volumetric Deformation Energy

Minimize similar energies to surface case \[ \int_{\R^3} \norm{\vec{d}_{uu}}^2+ \norm{\vec{d}_{uv}}^2+ \ldots + \norm{\vec{d}_{ww}}^2 \,\func{d}V \; \to \; \min \]
But displacement function now lives in 3D…
- Need a volumetric space tessellation?
- No, same functionality provided by RBFs

Radial Basis Functions

Represent deformation by RBFs \[ \vec{d}\of{\vec{x}} = \sum_j \vec{w}_j \, \phi\of{\norm{\vec{c}_j - \vec{x} }} \]
Triharmonic basis function \(\phi(r)=r^3\)
- Satisfy \(\laplace^3 \vec{d}=\vec{0}\) by construction
- Therefore the deformaton minimizes \[ \int_{\R^3} \norm{\vec{d}_{uuu}}^2+ \norm{\vec{d}_{vuu}}^2+ \ldots + \norm{\vec{d}_{www}}^2 \,\func{d}u\,\func{d}v\,\func{d}w \]
- Leads to very smooth and fair deformations

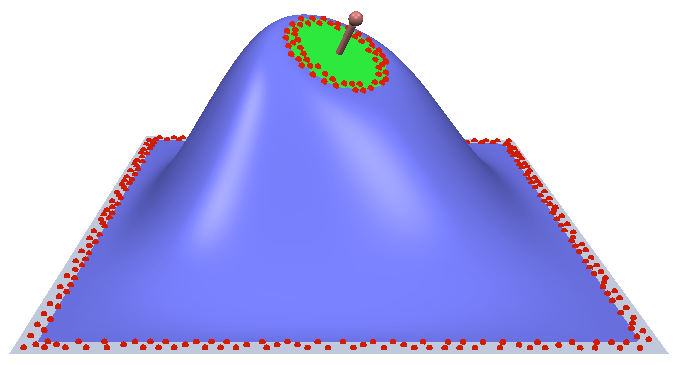
RBF Deformation

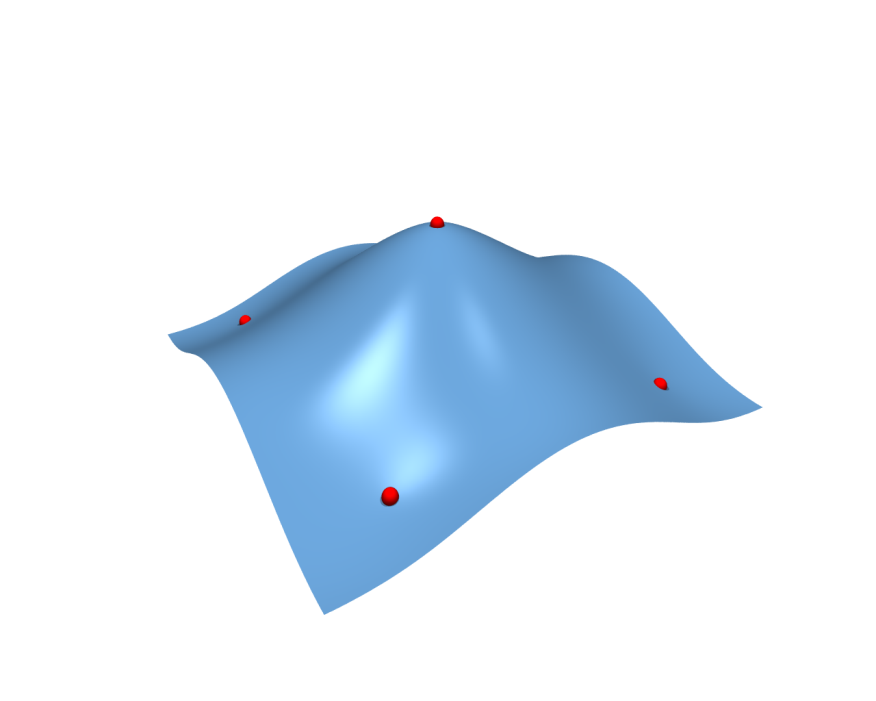
Represent deformation by RBFs \[ \vec{d}\of{\vec{x}} = \sum_{j=1}^n \vec{w}_j \, \phi\of{\norm{\vec{c}_j - \vec{x} }} \]

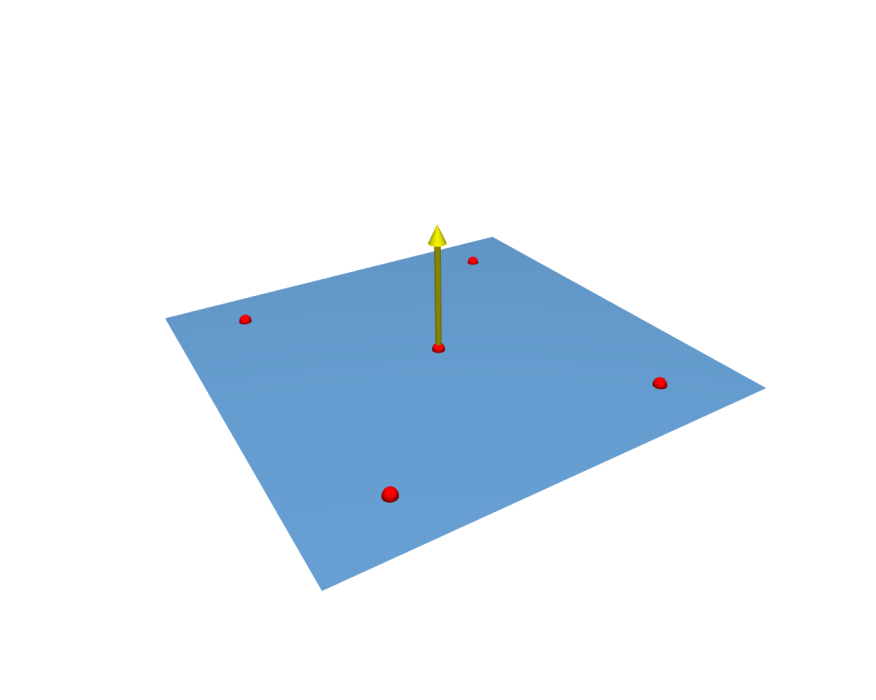
Preprocessing: RBF fitting
- Interpolate constraints: 2 rings of vertices at region boundaries (red points)
- Solve dense \(n \times n\) linear system for \(\vec{w}_j\)
Deformation: RBF evaluation
- Function \(\vec{d}\) transforms all points \(\vec{x}_i\), its Jacobian \(\left( \grad \vec{d} \right)^{-\mathsf{T}}\) transforms normals \(\vec{n}_i\)
- Evaluation can be implemented highly parallel with GPU shaders