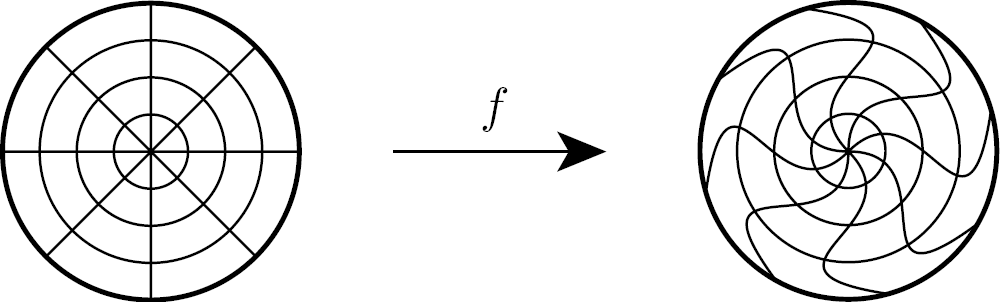
Overview
- Motivation
- Recap: Differential Geometry
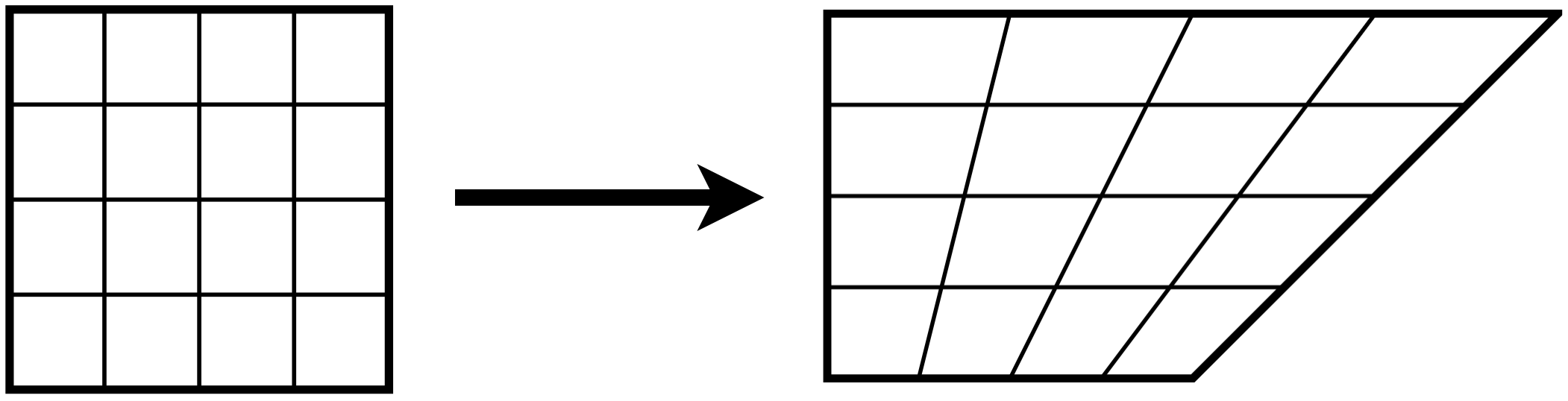
- Classification of Mappings
- Harmonic Functions
- Discrete Harmonic Maps
- Advanced Methods
Motivation
- Texture Mapping
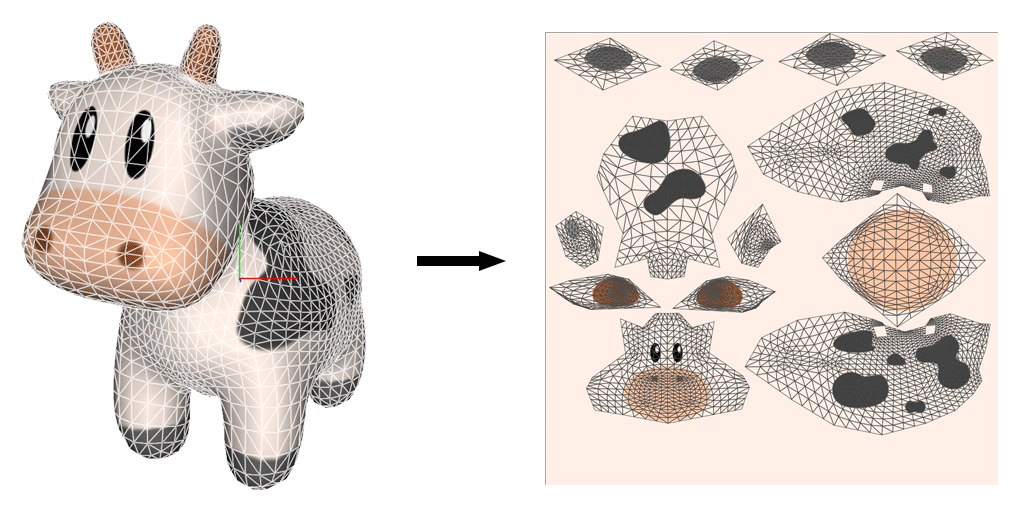
Motivation
- Normal Mapping
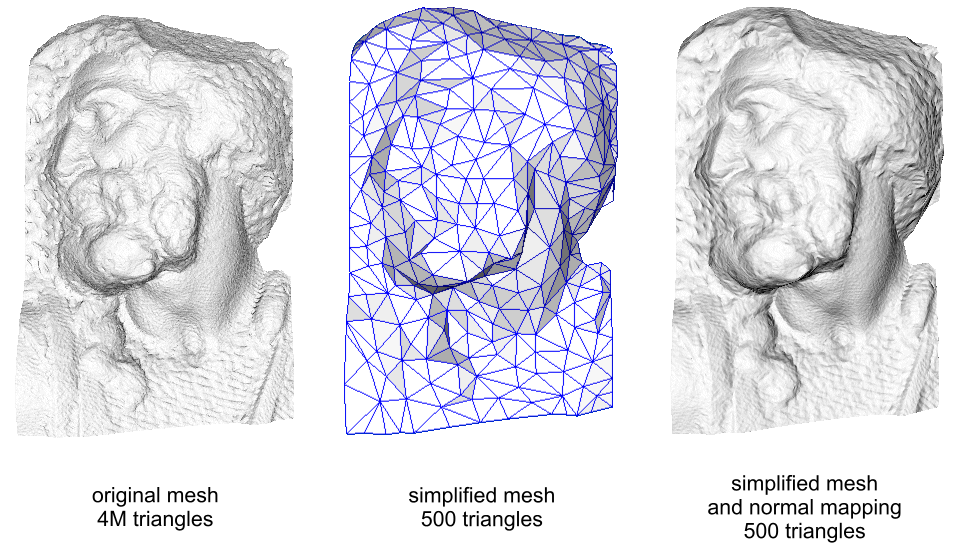
Motivation
- Remeshing
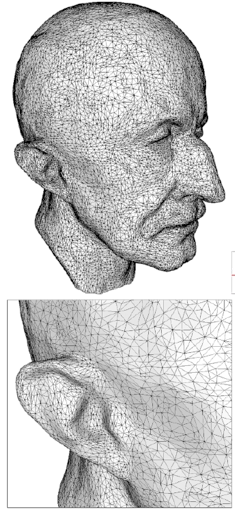
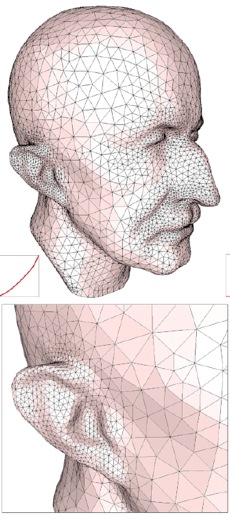
Alliez et al.: Interactive Geometry Remeshing - SIGGRAPH 2002
Motivation
- Shape Interpolation

Kraevoy,Sheffer: Cross-Parameterization and Compatible Remeshing of 3D Models - SIGGRAPH 2004
Motivation
- Geometric pattern synthesis

Dumas,Lu,Lefebvre,Wu,Dick: By-Example Synthesis of Structurally Sound Patterns - SIGGRAPH 2015
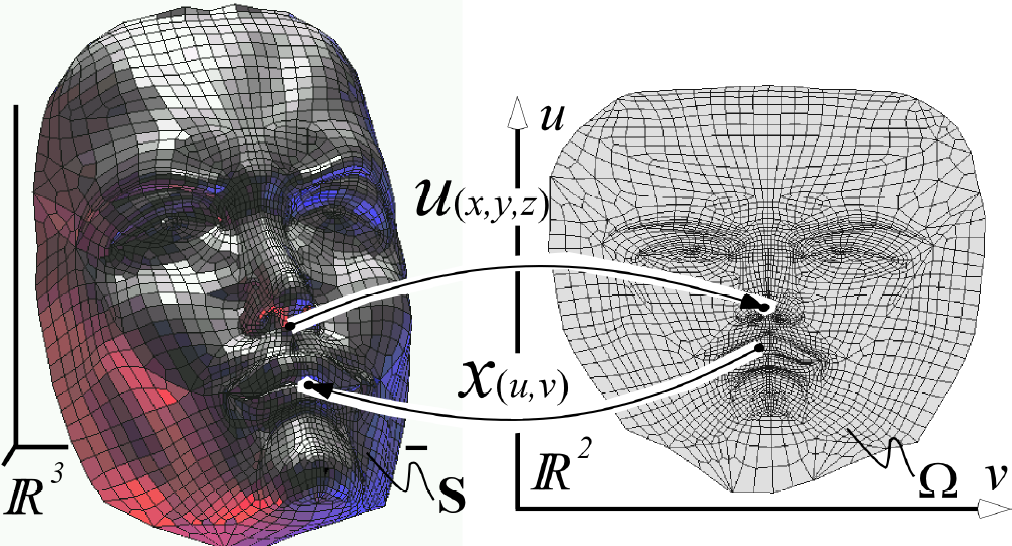
Mesh Parameterization
- Find a one-to-one (bijective) mapping between a given surface mesh and a 2D parameter domain
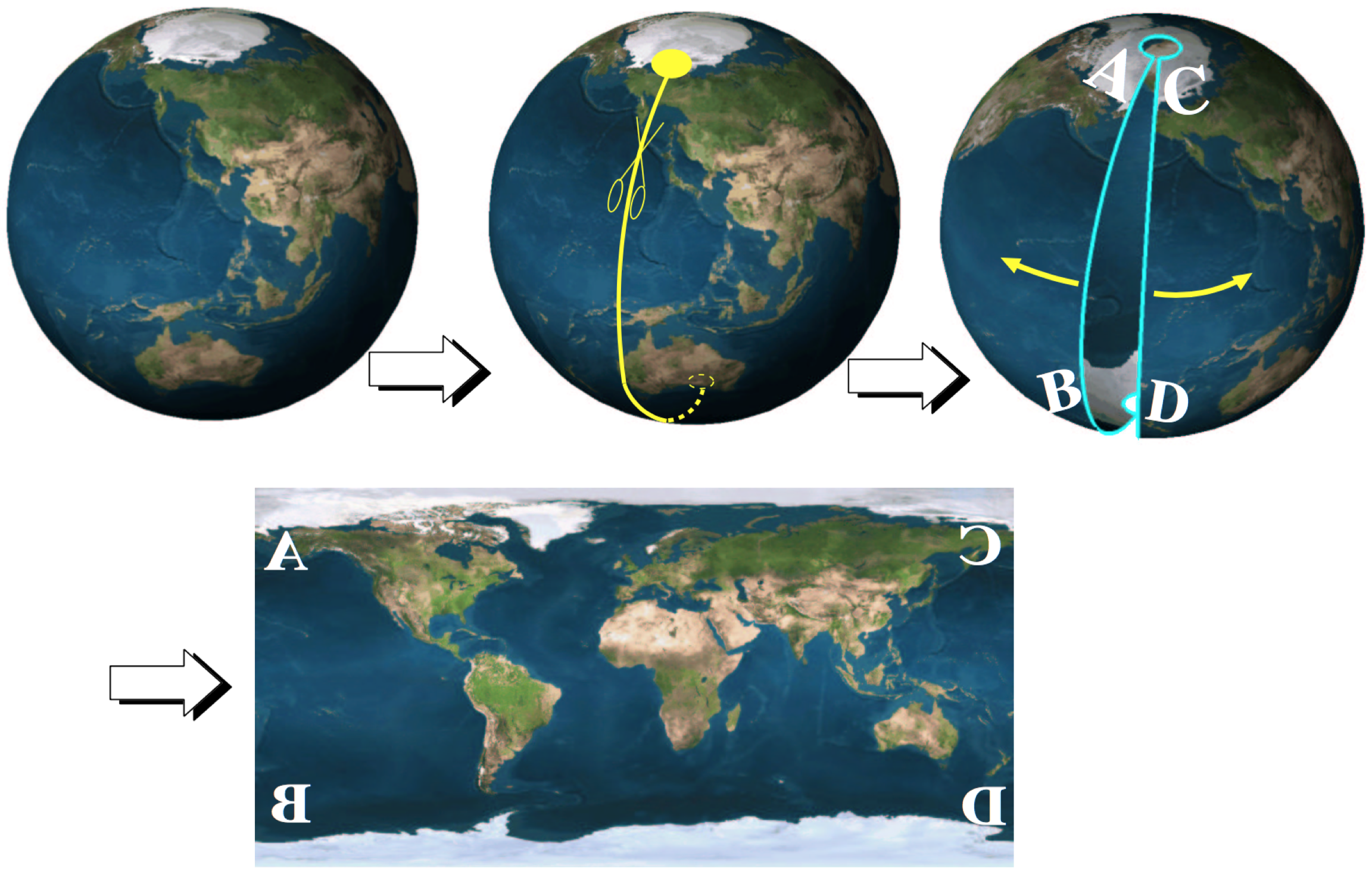
Unfolding the World
Spherical Coordinates
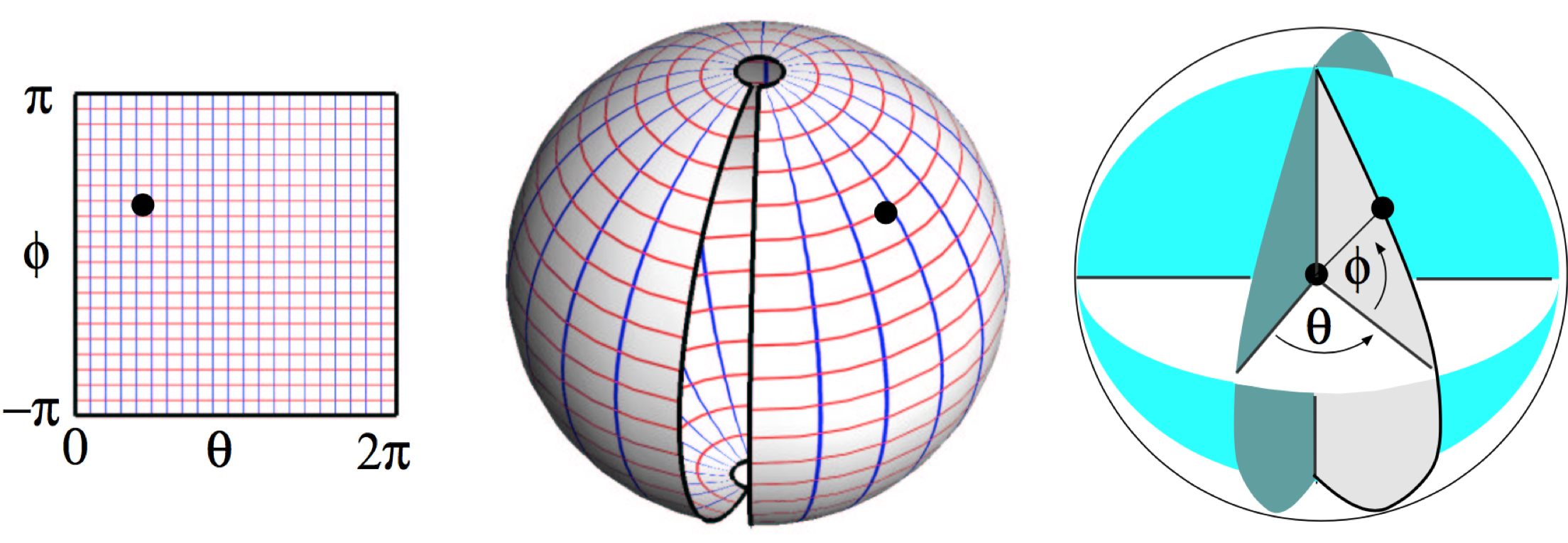
\[ \matrix{\theta \\ \phi} \mapsto \matrix{\sin \theta \sin \phi \\ \cos \theta \ \sin\phi \\ \cos \phi} \]
Desirable Properties
- Bijective mapping


- Low distortion
- How to measure distortion?
- Can distortion be avoided completely?

Cartography
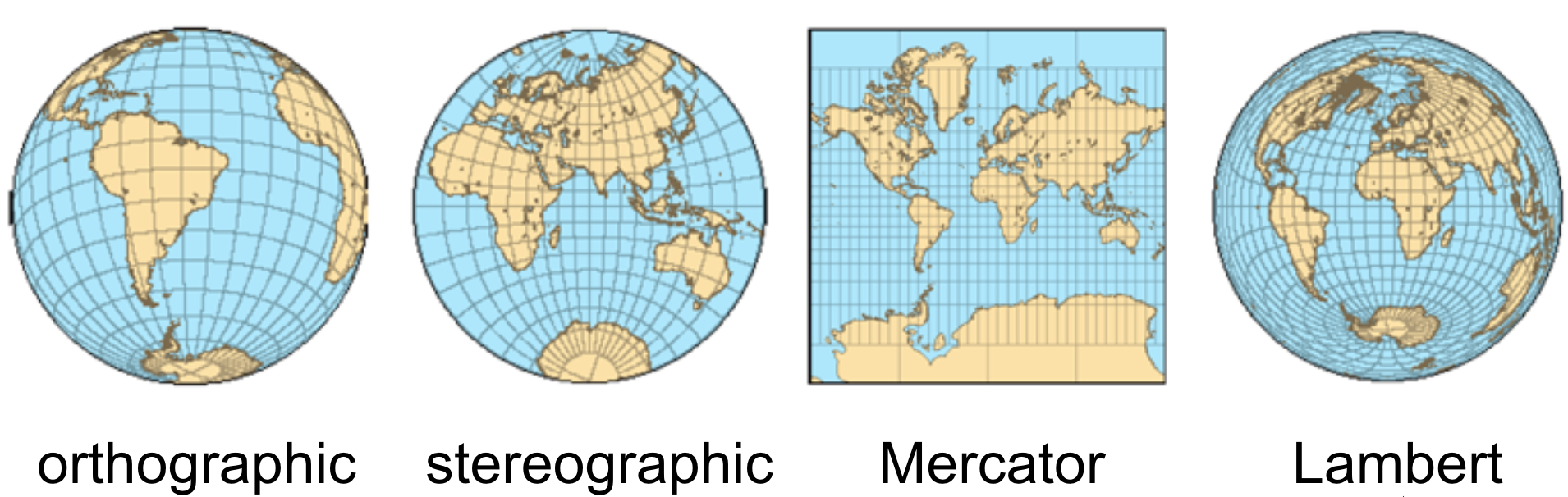
Floater, Hormann: Surface Parameterization: A Tutorial and Survey, 2005
More Maps


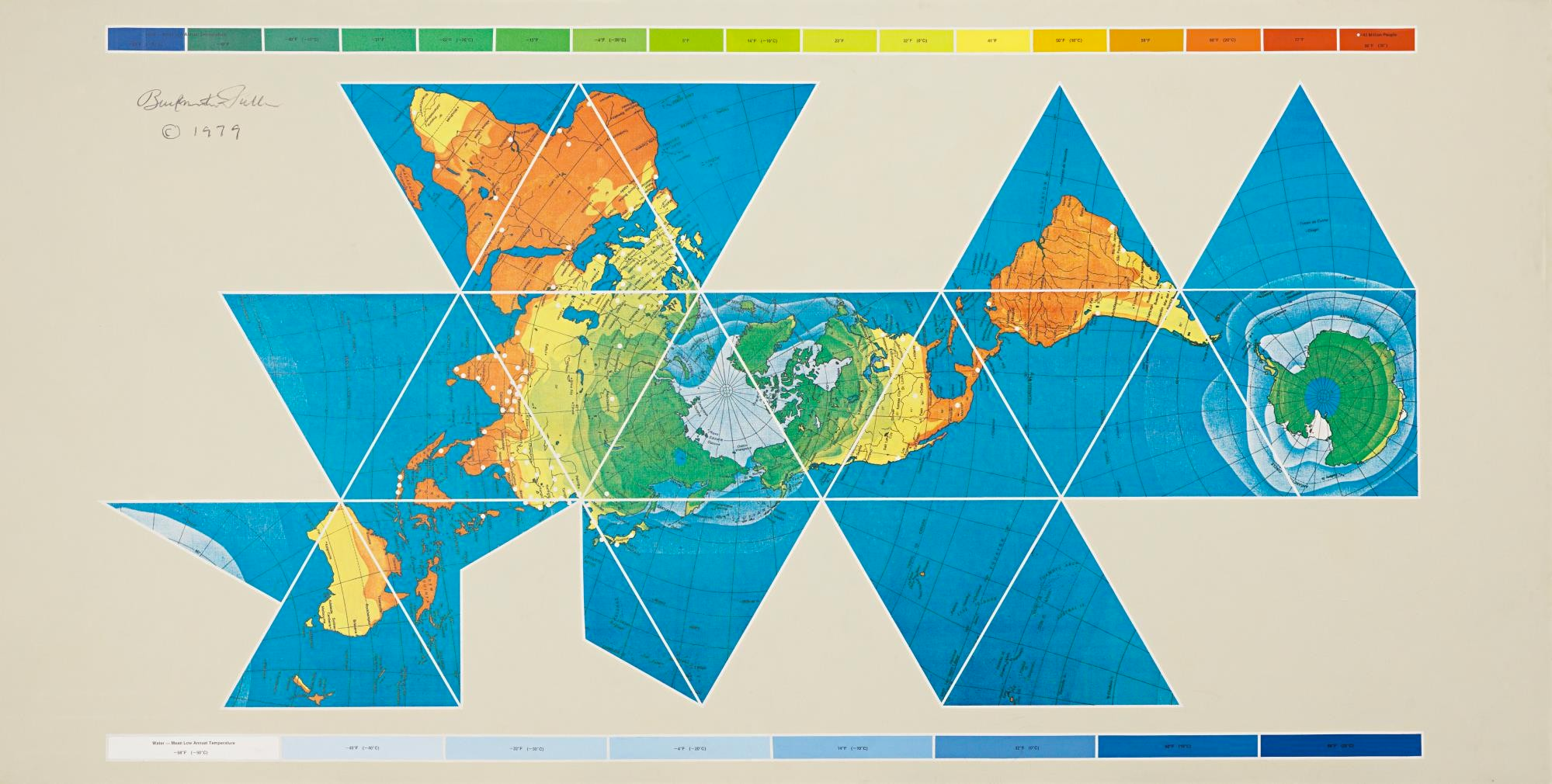
Dymaxion Map
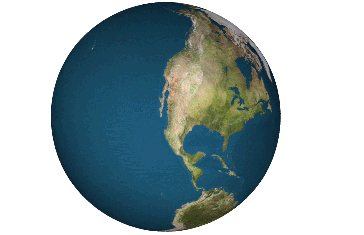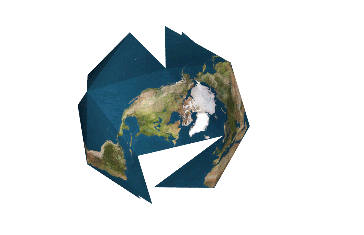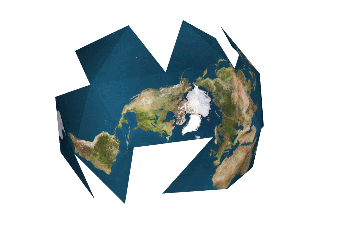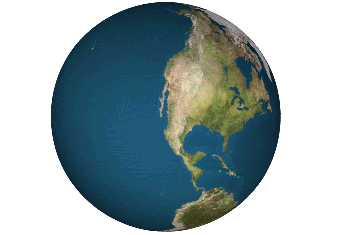
Dymaxion Map
New Maps
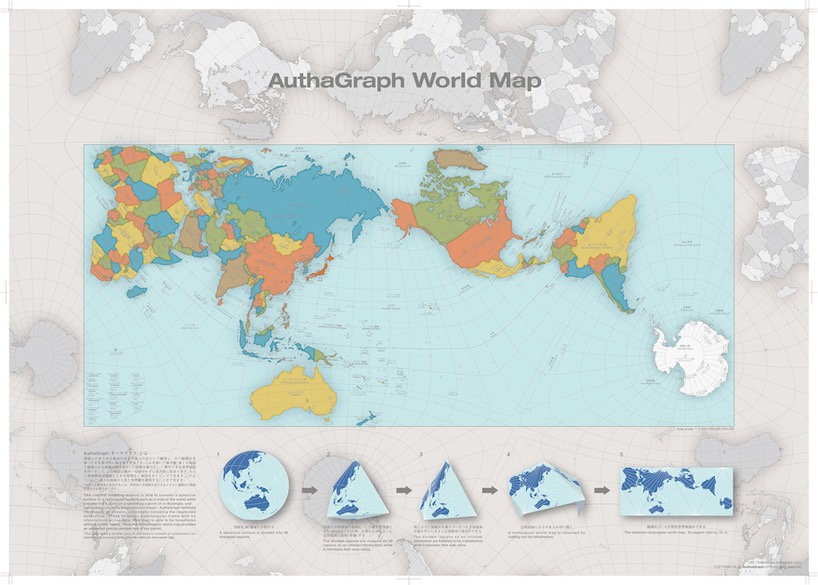
Authagraph by hajime narukawa wins 2016 japan GOOD DESIGN grand award
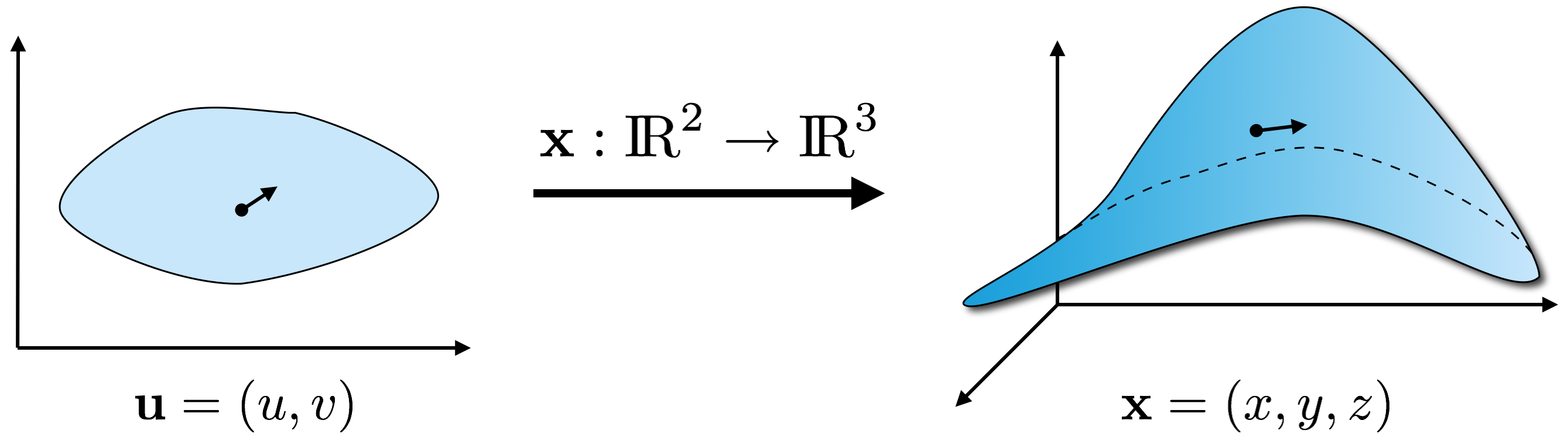
Differential Geometry
- Parametric surface representation
\[ \begin{eqnarray} \vec{x} \colon \Omega \subset \R^2 & \to & \set{S} \subset \R^3 \\[2mm] \of{u,v} & \mapsto & \matrix{x\of{u,v} \\ y\of{u,v} \\ z\of{u,v}} \end{eqnarray} \]
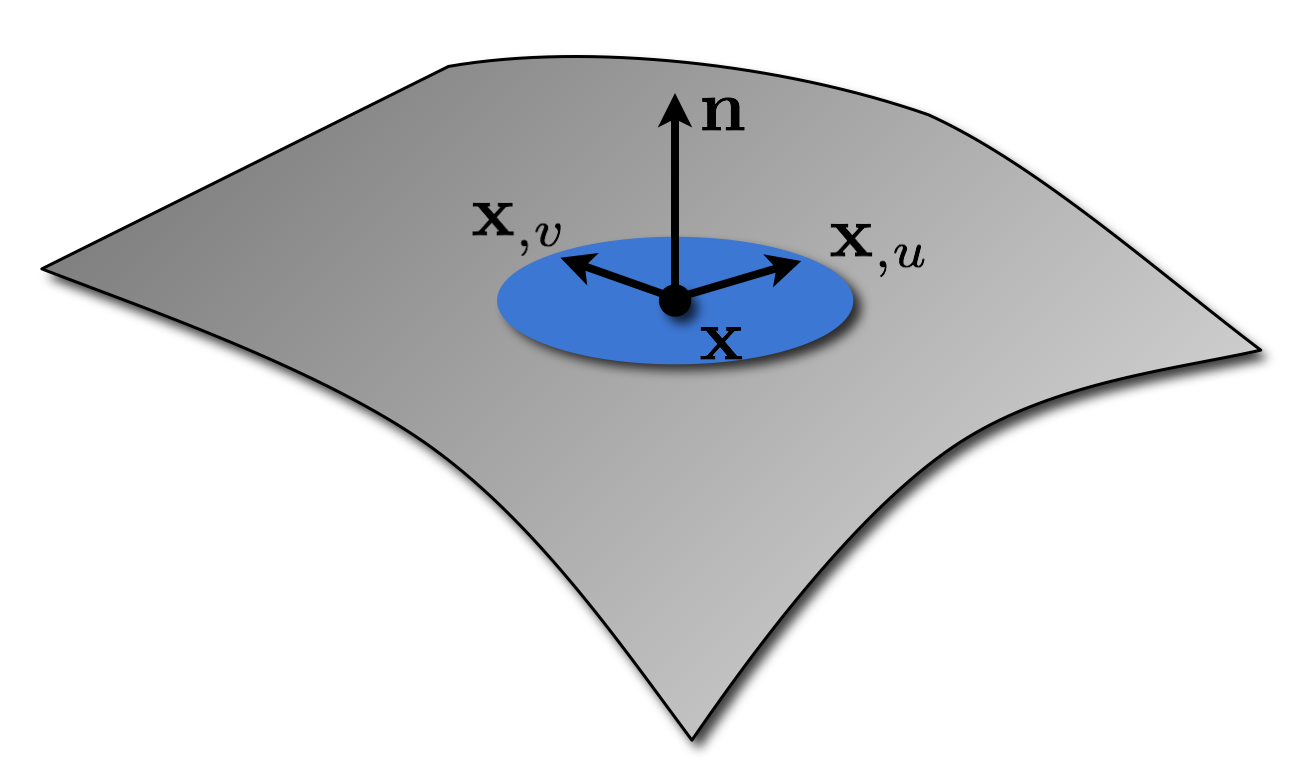
- Regular if
- Coordinate functions \(x\), \(y\), \(z\) are smooth
- Tangents are linearly independent: \(\vec{x}_{,u} \times \vec{x}_{,v} \neq \vec{0}\)
Distortion Analysis
- Jacobian transforms infinitesimal vectors
\[ \func{d}\vec{x} = \mat{J} \func{d}\vec{u} \quad \quad \mat{J} = \matrix{ x_u & x_v \\ y_u & y_v \\ z_u & z_v } \]
\[\norm{\func{d}\vec{x}}^2 \;=\; \left(\func{d}\vec{u} \right)^T \mat{J}^T \mat{J} \, \func{d}\vec{u} \;=\; \left(\func{d}\vec{u} \right)^T \mat{I} \, \func{d}\vec{u} \]
First Fundamental Form
- Characterizes the surface metric locally
\[\vec{I} \;=\; \matrix { \vec{x}_u^T \vec{x}_u & \vec{x}_u^T \vec{x}_v \\ \vec{x}_u^T \vec{x}_v & \vec{x}_v^T \vec{x}_v } \]
- Allows to measure on the surface
- Angles: \(\cos\theta \;=\; \left( \func{d}\vec{u}_1^T \, \mat{I} \, \func{d}\vec{u}_2 \right) / \left( \norm{\func{d}\vec{u}_1} \cdot \norm{\func{d}\vec{u}_2} \right)\)
- Length: \(\func{d}s^2 \;=\; \func{d}\vec{u}^T \, \mat{I} \, \func{d}\vec{u}\)
- Area: \(\func{d}A \;=\; \func{det}\of{\mat{I}} \,\func{d}u\,\func{d}v\)
First Fundamental Form
- Example \(\vec{f},\vec{g} \colon [0,1]^2 \to \R^3\)
\[\vec{f}(u,v) = \matrix{\sin u \\ \cos u \\ v} \]

\[\vec{g}(u,v) = \matrix{\sin u \\ \cos u \\ v^2} \]

First Fundamental Form
- Example \(\vec{f},\vec{g} \colon [0,1]^2 \to \R^3\)
\[\vec{f}(u,v) = \matrix{\sin u \\ \cos u \\ v} \]
\[\vec{f}_{,u} = \matrix{\cos u \\ -\sin u \\ 0} \quad \vec{f}_{,v} = \matrix{0 \\ 0 \\ 1}\]
\[\vec{g}(u,v) = \matrix{\sin u \\ \cos u \\ v^2} \]
\[\vec{g}_{,u} = \matrix{\cos u \\ -\sin u \\ 0} \quad \vec{g}_{,v} = \matrix{0 \\ 0 \\ 2v}\]
First Fundamental Form
- Example \(\vec{f},\vec{g} \colon [0,1]^2 \to \R^3\)
\[\vec{f}(u,v) = \matrix{\sin u \\ \cos u \\ v} \]
\[\vec{I_f}(u,v) = \matrix{1 & 0 \\ 0 & 1 } \]
\[\vec{g}(u,v) = \matrix{\sin u \\ \cos u \\ v^2} \]
\[\vec{I_g}(u,v) = \matrix{1 & 0 \\ 0 & 4v^2 }\]
First Fundamental Form
- Example \(\vec{f},\vec{g} \colon [0,1]^2 \to \R^3\)
\[\vec{f}(u,v) = \matrix{\sin u \\ \cos u \\ v} \]

\[\vec{g}(u,v) = \matrix{\sin u \\ \cos u \\ v^2} \]

Definitions
A regular parameterization \(\vec{x} \colon \Omega \to \set{S}\) is
- conformal (angle preserving), if the angle of every pair of intersecting curves on \(\set{S}\) is the same as that of the corresponding pre-images in \(\Omega\).
- equiareal (area preserving) if every part of \(\Omega\) is mapped onto a part of \(\set{S}\) with the same area
- isometric (length preserving), if the length of any arc on \(\set{S}\) is the same as that of its pre-image in \(\Omega\).
Cartography

Floater, Hormann: Surface Parameterization: A Tutorial and Survey, 2005
= conformal
= equiareal
Isometric Maps
- A regular parameterization \(\vec{x}(u,v)\) is isometric, iff its first fundamental form is the identity: \[\mat{I}\of{u,v} \;=\; \matrix{ 1 & 0 \\ 0 & 1 }\]
- A surface can have an isometric parameterization, iff it has zero Gaussian curvature.
- Which surfaces with zero Gaussian curvature do you know?
Conformal Maps
- A regular parameterization \(\vec{x}(u,v)\) is conformal, iff its first fundamental form is a scalar multiple of the identity:
\[\mat{I}\of{u,v} \;=\; s\of{u,v} \cdot \matrix{ 1 & 0 \\ 0 & 1 }\]
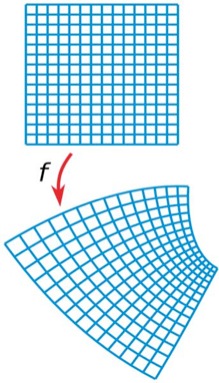
Conformal Maps
- Riemann Conformal Mapping Theorem
- Any two simply connected compact planar regions can be mapped conformally onto each other
- Close relationship to circle packings
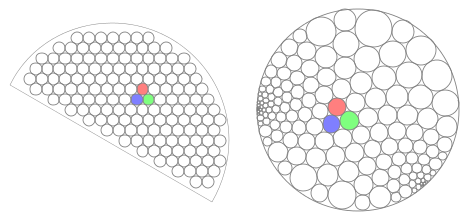
Conformal Maps

Conformal Flow

Crane et al. Spin Transformations of Discrete Surfaces, ACM Siggraph 2011
Equiareal Maps
- A regular parameterization \(\vec{x}(u,v)\) is equiareal, iff the determinant of its first fundamental form is 1:
\[ \det\of{\mat{I}\of{u,v}} \;=\; 1 \]
Relationships
- An isometric parameterization is conformal and equiareal, and vice versa:
isometric ⇔ conformal + equiareal
- Isometric is ideal, but rare. In practice, people try to compute:
- Conformal
- Equiareal
- Some balance between the two
Example
- Least-Squares Conformal Map
- tries to minimize angle distortion and non-uniform scalings
- implemented in many tools, e.g. matlab, blender, meshlab, libigl, etc.
Levy et al.: Least squares conformal maps for automatic texture atlas generation - SIGGRAPH 2002
Harmonic Functions on Surfaces
- A function \(\vec{f} \colon \set{S} \to \R^n\) on a surface \(\set{S}\) is harmonic if it satisfies (for each coordinate) \[\laplace_{\set{S}} \vec{f} \;=\; 0\]
- A harmonic function minimizes the Dirichlet energy given suitable boundary conditions \[E_D(\vec{f}) = \int_{\set{S}} \norm{ \grad_{\set{S}} \vec{f} }^2 \func{d}A\]
Harmonic Maps
- Isometric maps are conformal, conformal maps are harmonic:
isometric ⇒ conformal ⇒ harmonic - Harmonic maps are easier to compute than conformal maps
- Harmonic maps are not conformal in general, i.e. do not necessarily preserve angles
Harmonic Maps
Theorem [Rado-Kneser-Choquet]
If \(\vec{f} \colon \set{S} \to \R^2\) is harmonic and maps the boundary \(\partial \set{S}\) of \(\set{S}\) homeomorphically onto the boundary \(\partial \Omega\) of some convex region \(\Omega \subset \R^2\), then \(\vec{f}\) is bijective.
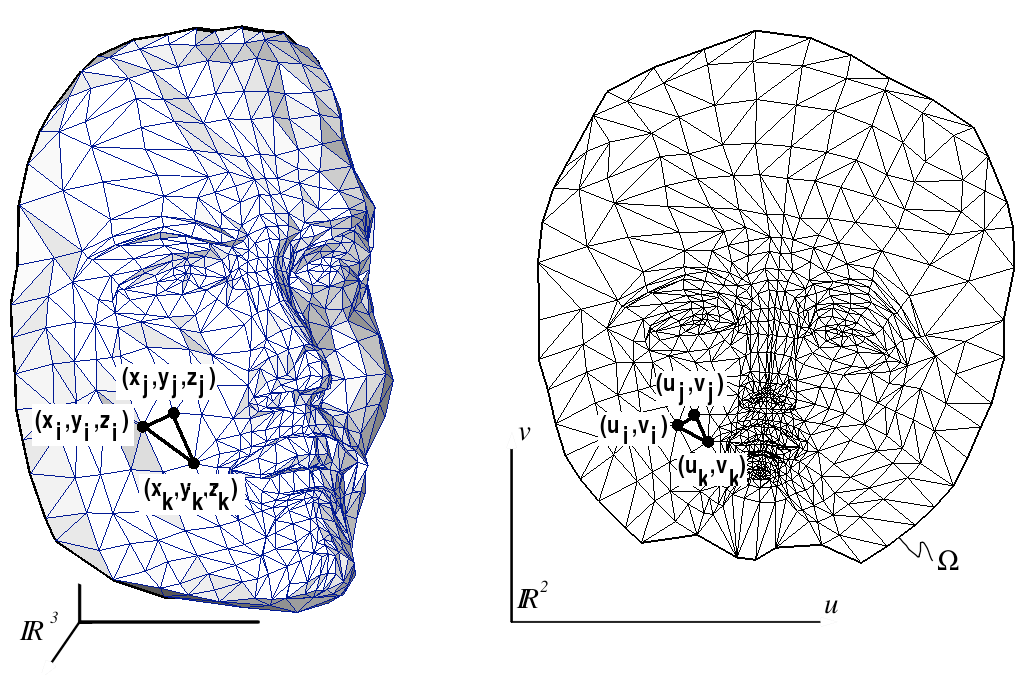
Discrete Maps
- Piecewise linear map of a discrete 3D triangle mesh onto a planar 2D polygon
- Given a mesh \(\set{S}\) compute the mapping \(\vec{u} \colon \set{S} \to \Omega \subset \R^2\), i.e., for each vertex \(v_i\) find parameter values \(\vec{u}_i \in \R^2\).
Discrete Harmonic Maps
- Map the boundary \(\partial \set{S}\) homeomorphically to some (convex) polygon \(\partial \Omega\) in the parameter plane
- Solve \(\laplace_{\set{S}} \vec{u} = 0\) through a linear system
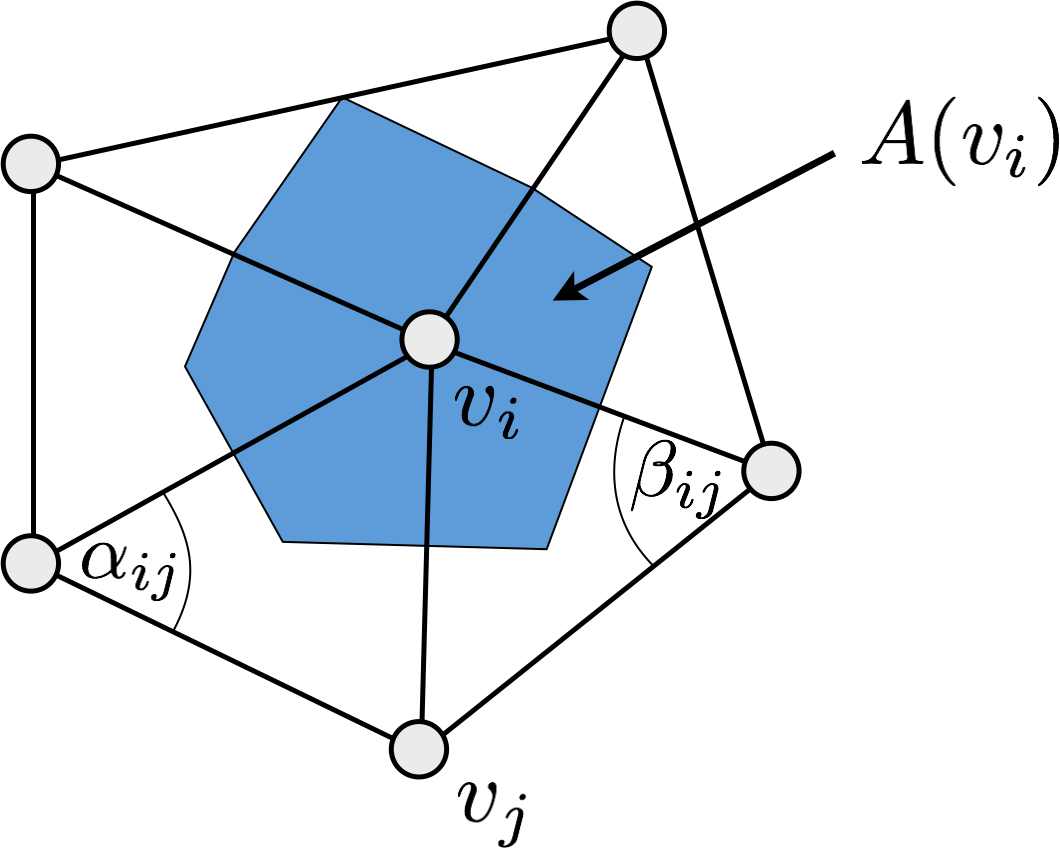
\[\forall v_i \in \set{S} \;:\; \sum_{v_j \in \set{N}_1\of{v_i}} w_{ij} \left( \vec{u}\of{v_j} - \vec{u}\of{v_i} \right) = 0\]
\[w_{ij} \;=\; \func{cot} \alpha_{ij} + \func{cot} \beta_{ij}\]
Example: Discrete Harmonic Map
- Uniform Laplace discretization \(w_{ij} = 1\)
- Boundary vertices: \(\{1,2,3,4\}\), interior vertices: \(\{5,6,7\}\)
- Map boundary to convex polygon (unit square)
Example: Discrete Harmonic Map
- Solve linear system \(\vec{L}\vec{u} = \vec{b}\) to find parameters \(\vec{u}\) \[ \tiny \mat{L} \;=\; \matrix{ 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 1 & -5 & 1 & 1\\ 1 & 0 & 0 & 1 & 1 & -4 & 1\\ 1 & 1 & 0 & 0 & 1 & 1 & -4\\ } \quad \mat{b} \;=\; \matrix{ 0 & 0\\ 1 & 0 \\ 1& 1 \\ 0 & 1 \\ 0 & 0 \\ 0& 0 \\ 0& 0} \quad \mat{u} \;=\; \matrix{ 0 & 0 \\ 1 & 0 \\ 1 & 1 \\ 0 & 1 \\ 0.53 & 0.53 \\ 0.25 & 0.45 \\ 0.45 & 0.25} \]
Discrete Harmonic Maps
- Importance of proper discretization of Laplace Operator


Discrete Harmonic Maps
- How to solve the linear system?
- Transform into symmetric positive definite system and solve it using conjugate gradients or sparse Cholesky
- Simply iterate the following for all vertices (why?) \[ \forall v_i \in \set{S} \;:\; \vec{u}\of{v_i} \;\leftarrow\; \frac{1}{\sum_{v_j \in \set{N}_1\of{v_i}} w_{ij}} \sum_{v_j \in \set{N}_1\of{v_i}} w_{ij} \vec{u}\of{v_j}\]
- We will discuss both methods next week…
Try it yourself!
Discrete Harmonic Maps
- We know from the theorem of Rado-Kneser-Choquet that bijective harmonic maps onto convex domains exist.
- Does the same hold for discrete maps?
- Potential problems
- triangles could flip
- triangles could degenerate to zero area
Convex Combination Maps
- A discrete mapping that satisfies the linear equations
\[\sum_{v_j \in \set{N}_1\of{v_i}} w_{ij} \left( \vec{u}\of{v_j} - \vec{u}\of{v_i} \right) = 0\]
\(\;\;\;\) and has positive weights that sum to one, i.e.
\(\;\;\;\) is called a convex combination mapping.
Convex Combination Maps
- Each \(\vec{u}(v_i)\) is a convex combination of \(\vec{u}(v_j)\)
\[ \vec{u}\of{v_i} \;=\; \sum_{v_j \in \set{N}_1\of{v_i}} w_{ij} \vec{u}\of{v_j}\]
- Theorem [Tutte]:
If \(\vec{u} \colon \set{S} \to \Omega\) is a convex combination map that maps the boundary \(\partial \set{S}\) homeomorphically to the boundary \(\partial \Omega\) of a convex region \(\Omega \subset \R^2\), then \(\vec{u}\) is one-to-one.
Convex Combination Maps
- Uniform barycentric weights \[ w_{ij} \;=\; 1 / \func{valence}\of{v_i}\]
- Cotangent weights (\(> 0\) only if \(\alpha_{ij} + \beta_{ij} < \pi\)!) \[w_{ij} \;=\; \cot\of{\alpha_{ij}} + \cot\of{\beta_{ij}}\]

- Mean value weights (always > 0) \[w_{ij} \;=\; \frac{ \tan\of{\delta_{ij}/2} + \tan\of{\gamma_{ij}/2} } {\norm{ \vec{x}_j - \vec{x}_i }}\]
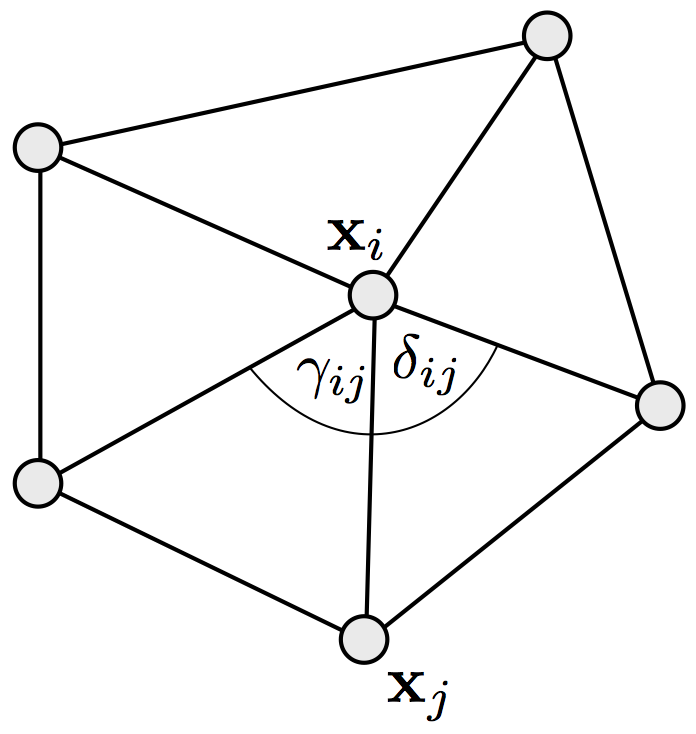
Convex Combination Maps
- Comparison
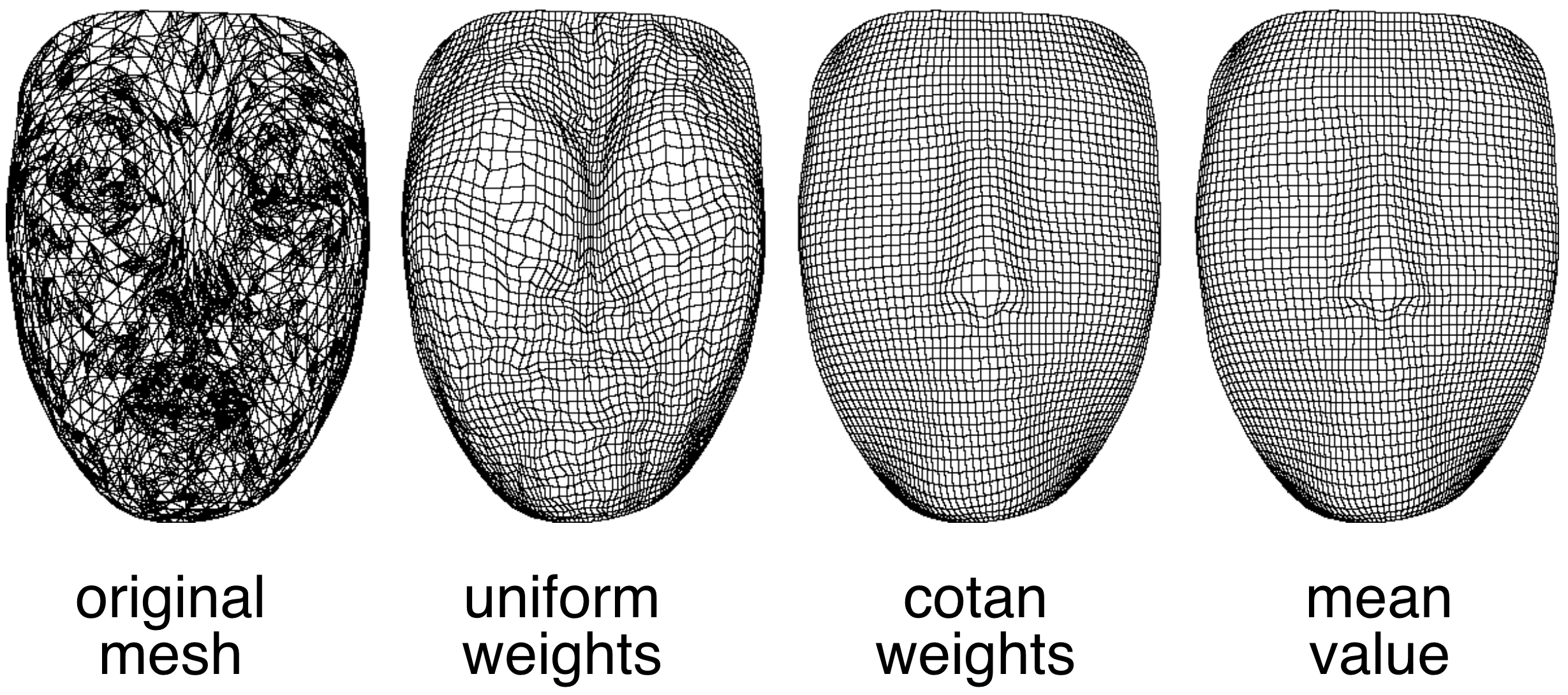
Try it yourself!
Fixing the Boundary
- Basic Approach
- Choose a simple convex shape, e.g. triangle, square, circle
- Distribute points on boundary, e.g. use arc length parameterization
- Solve Laplace equation
- Problem: Fixing the boundary can create high distortion






Open Boundary Mappings
- Include boundary vertices in the optimization
- Produces mappings with lower distortion

Open Boundary Mappings
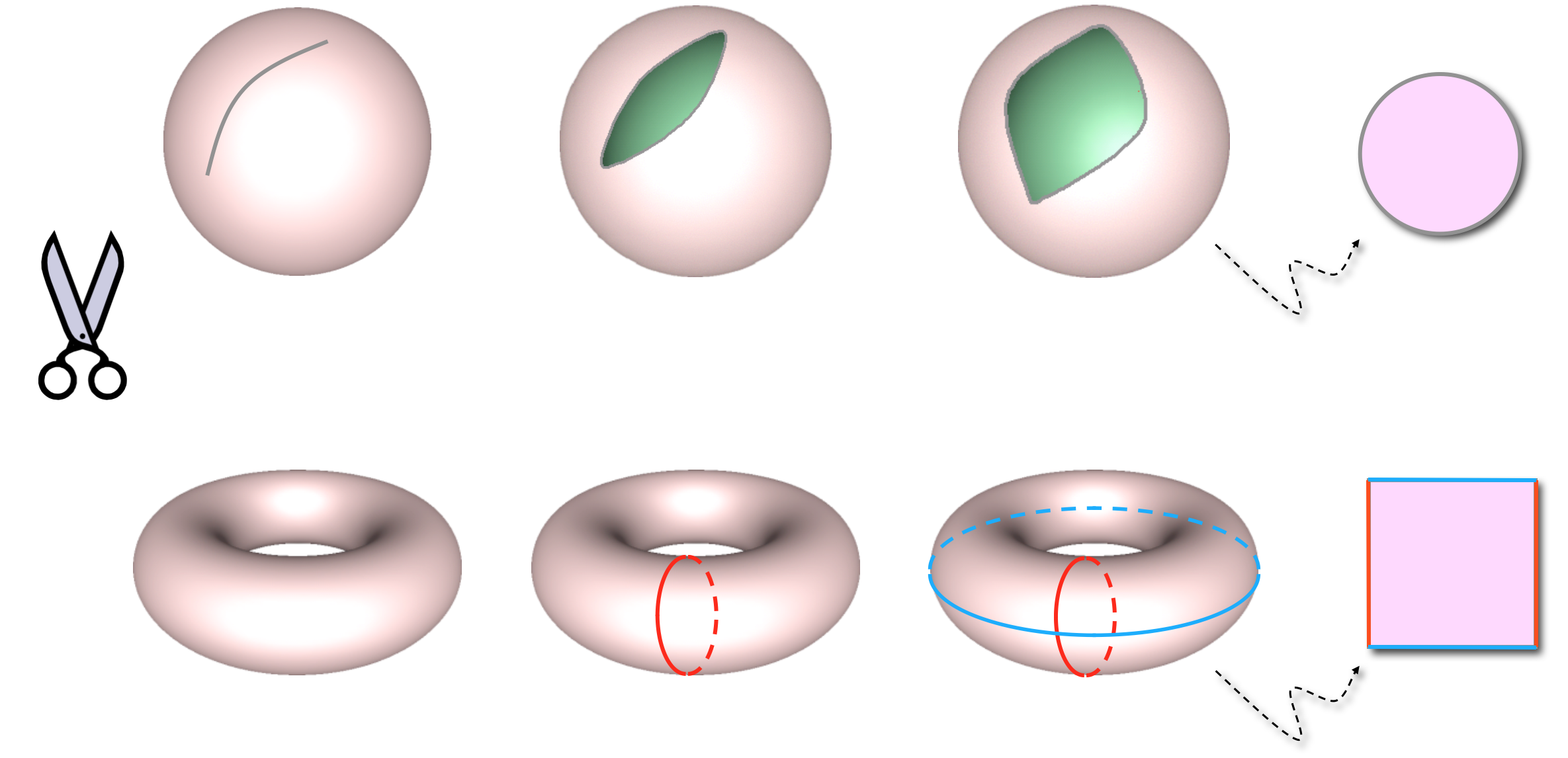
- Need disk-like topology
- Introduce cuts on the mesh
Open Boundary Mappings
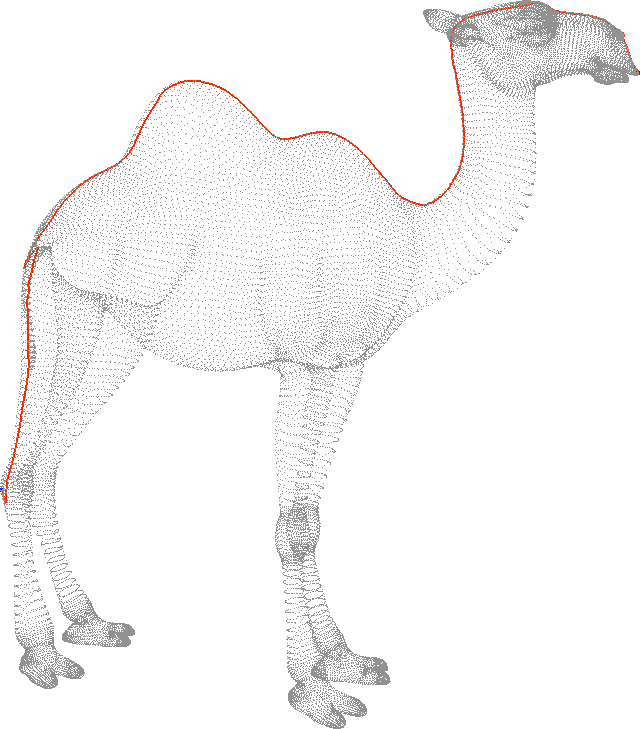
- Need disk-like topology
- Introduce cuts on the mesh
- Naive cut introduces large distortions
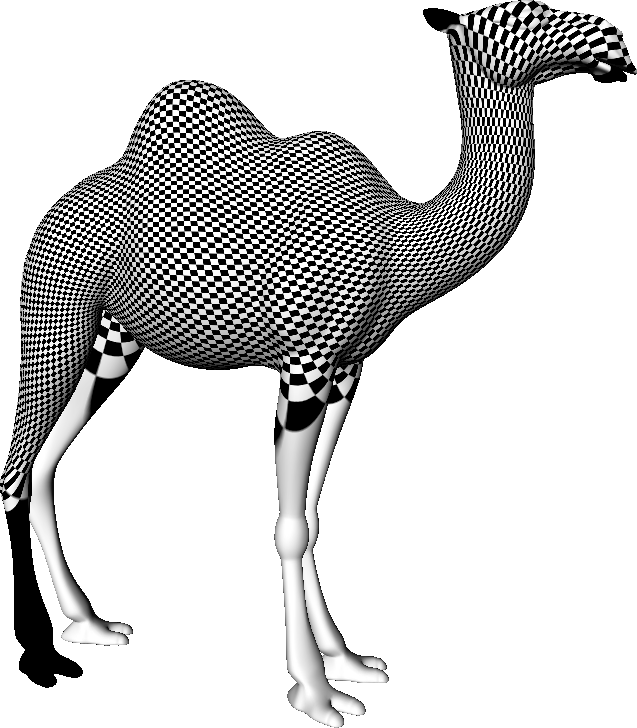
Open Boundary Mappings
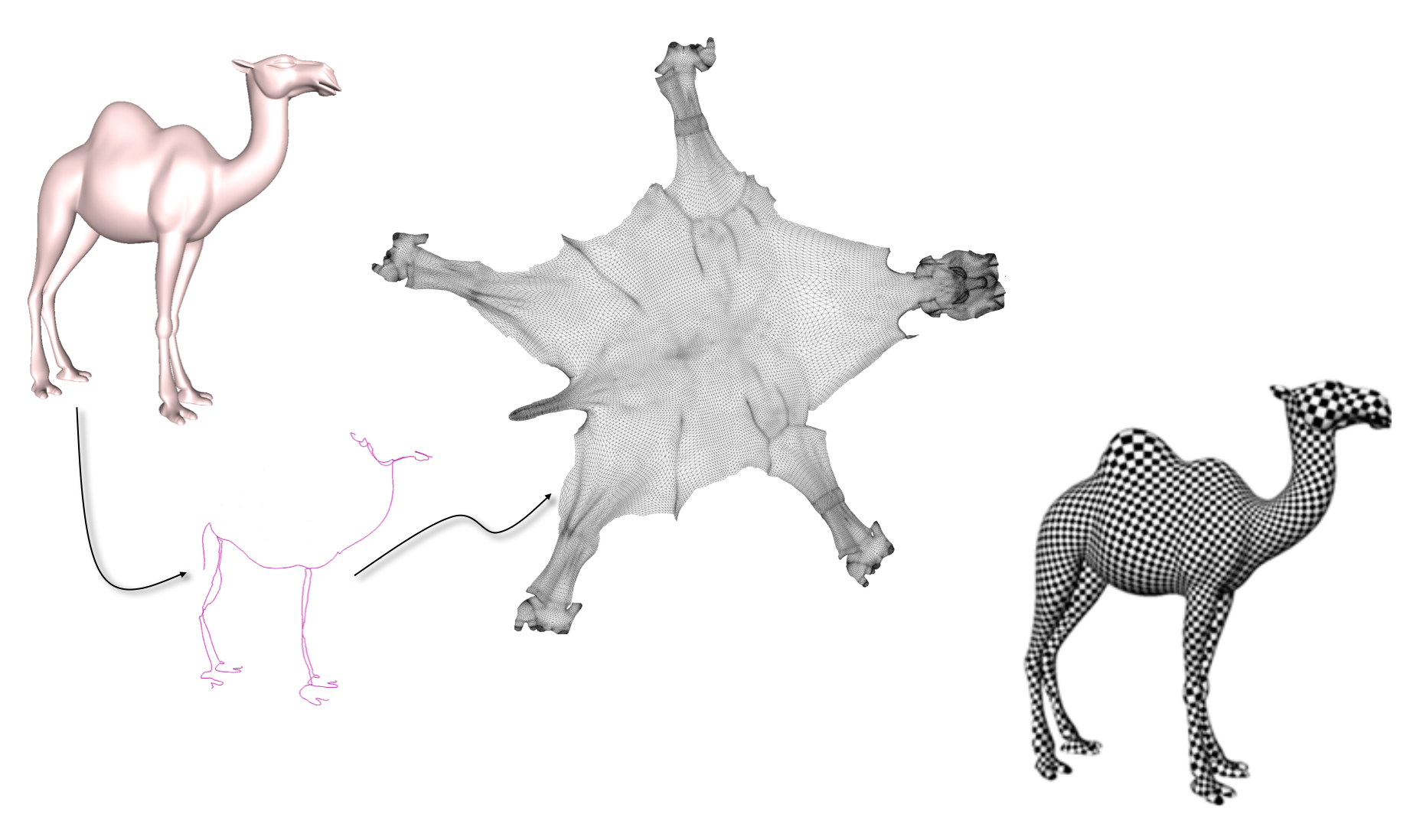
- Need disk-like topology
- Introduce cuts on the mesh
- Smart cuts reduce distortion
Texture Atlas Generation
- Split model into number of patches (atlas)
- to reduce distortion
- to avoid self-intersections
- to improve texture packing
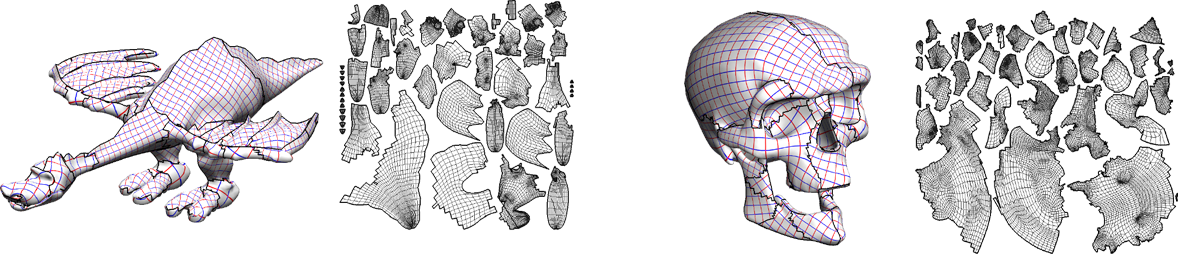
Levy et al.: Least squares conformal maps for automatic texture atlas generation - SIGGRAPH 2002
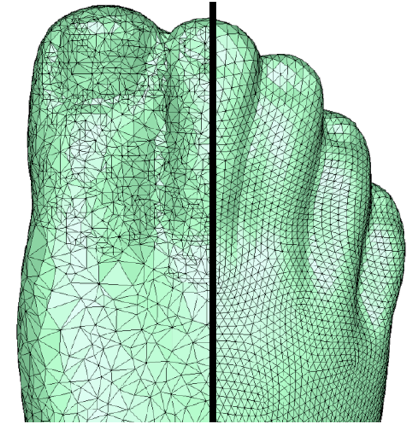
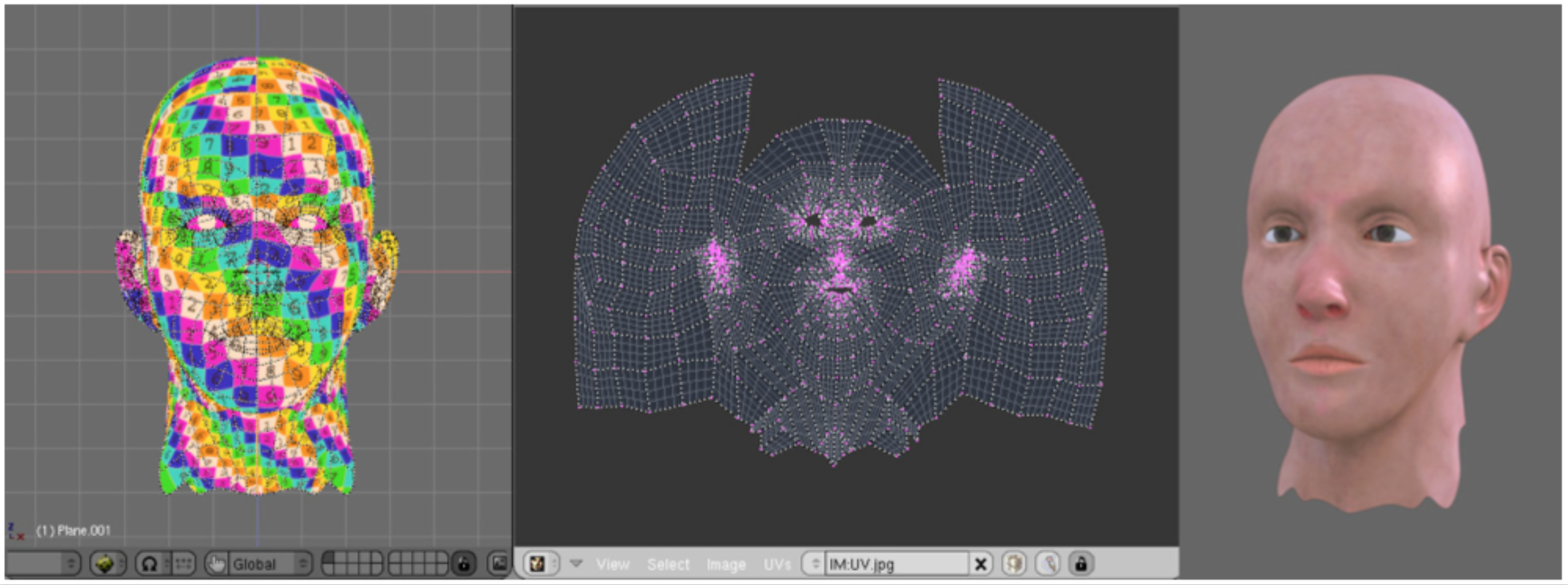
Real-World Example


Real-World Example


Real-World Example
Literature
- Botsch et al., Polygon Mesh Processing, AK Peters, 2010
- Chapter 5

- Floater & Hormann, Surface Parameterization: A Tutorial and Survey, Advances in Multiresolution for Geometric Modeling, Springer 2005
- has all the concepts
- Hormann et al., Mesh Parameterization, Theory and Practice, SIGGRAPH 2007 Course
- has all the proofs