Overview
- Topology
- Genus
- Euler formula
- Platonic solids
- Remeshing
- Local mesh adaptation
- Iterative remeshing algorithm
Global Topology
- Genus
- Maximal number of closed simple cutting curves that do not disconnect the graph into multiple components
- Informally, the number of holes or handles



Euler Formula
- For a closed polygonal mesh of genus \(g\), the relation of the number \(V\) of vertices, \(E\) of edges, and \(F\) of faces is given by Euler’s formula
\[ V-E+F = 2(1-g)\]
- The term \(2(1-g)\) is called Euler characteristic \(χ\) and only depends on the topological structure, not on the geometric shape nor the triangulation
Euler Formula
- Typically, \(V\), \(E\), \(F\) are large and \(g\) is small \[ V-E+F = 2(1-g) \approx 0 \]
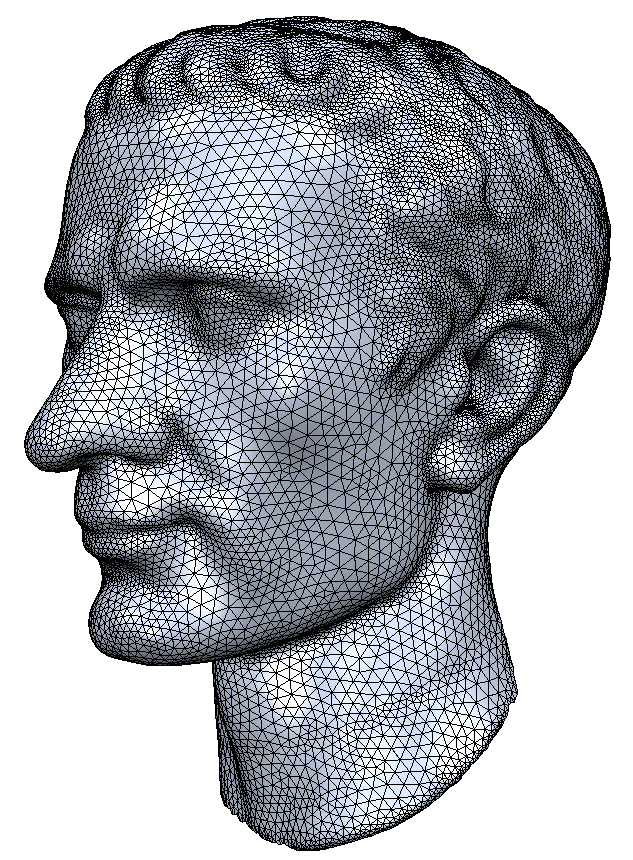
- Split edges into halfedges
\[ H = 2E \]
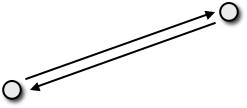
- Focus on triangle meshes \[ H = 3F \]
Euler Formula
- Express \(E\) in terms of \(F\) \[ V - \frac{3}{2}F + F \approx 0 \quad\Rightarrow\quad F \approx 2V \]
- Express \(F\) in terms of \(E\) \[ V - E + \frac{2}{3}E \approx 0 \quad\Rightarrow\quad E \approx 3V \]
- Valence/degree: How many incident halfedges per vertex?
\[ E \approx 3V \quad\Rightarrow\quad H \approx 6V \]
Example: Stanford Bunny

Mesh Statistics
- Triangle Meshes
- \(F \approx 2V\)
- \(E \approx 3V\)
- Average valence 6
- Quad Meshes
- \(F \approx V\)
- \(E \approx 2V\)
- Average valence 4

Soccer Ball
- How many pentagons are in a soccer ball?

- Any closed surface of genus zero consisting only of hexagons and pentagons and where every vertex has valence 3 must have exactly 12 pentagons!
Platonic Solids
- Platonic Solids
- Convex, regular 3D polyhedra
- Faces are regular and congruent

- Properties
- All faces are convex, regular \(p\)-gons
- All angles are equal
- All vertices have valence \(q\)

Platonic Solids
- How many platonic solids exist?
Geometric Proof
- Faces are regular \(p\)-gons
- \(p\) is at least 3
- Each face angle is \(\pi (1-2/p)\)
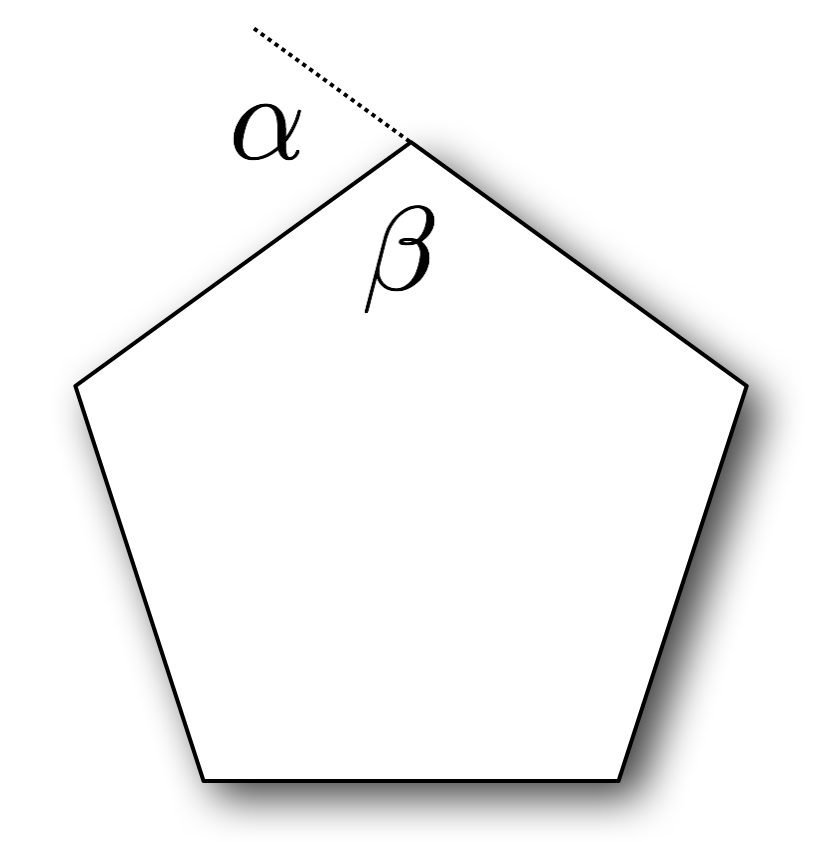
\[ \begin{eqnarray*} \alpha &=& 2\pi / p \\[2mm] \beta &=& \pi-\alpha \\ &=& \pi - 2\pi/p \\ &=& \pi (1-2/p) \end{eqnarray*}\]
- Vertices of valence \(q\)
- \(q\) is at least 3
- Sum of angles around a vertex is \(q \pi (1-2/p)\)
- Convexity: Angle sum \(q \pi (1-2/p) < 2 \pi\)
- Equivalent to \((p-2)(q-2) < 4\)
- Integer solutions with \(p, q \geq 3\):
- \(\{3,3\}, \{3,4\}, \{4,3\}, \{3,5\}, \{5,3\}\)
Topological Proof
- Euler formula tells us…
- Genus \(0 \; \rightarrow \; V - E + F = 2\)
- Valence \(q \; \rightarrow \; 2E = qV\)
- \(p\)-gons: \(\; \rightarrow \; 2E = pF\)
- Combine: \(\; \rightarrow \; 2E/q - E + 2E/p = 2\)
- Divide by \(2E \; \rightarrow \;1/q+ 1/p = 1/2 + 1/E\)
- Since \(E>0 \; \rightarrow \; 1/q+ 1/p > 1/2\)
- \(p, q \geq 3 \; \rightarrow \; \{3,3\}, \{3,4\}, \{4,3\}, \{3,5\}, \{5,3\}\)
Archimedean Solids
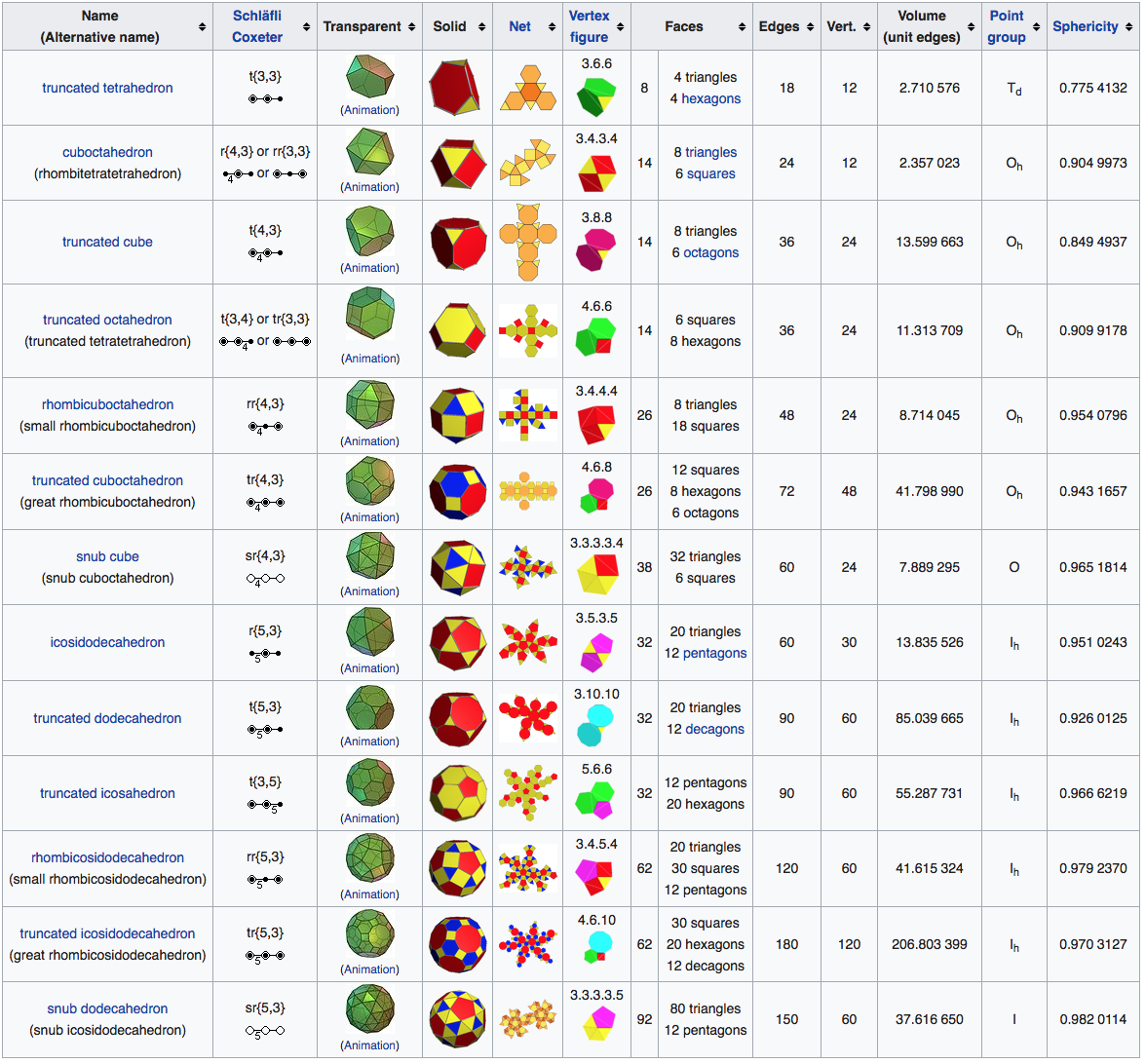
Fair Dice
- Platonic solids are fair dice

- Are there other fair dice?
- Yes!
Overview
- Topology
- Genus
- Euler formula
- Platonic solids
- Remeshing
- Local mesh adaptation
- Iterative remeshing algorithm
Remeshing
Remeshing
- Problem setting:
- “Given a 3D mesh, improve its triangulation while preserving its geometry.”
- Why?
- Robustness of numerical computations
- How?
- Avoid very small / large triangle angles
- Avoid very small / large triangle areas
- Book: Chapter 6
What is a good mesh?
- Equal edge lengths
- Equilateral triangles
- Valence close to 6

What is a good mesh?
- Equal edge lengths
- Equilateral triangles
- Valence close to 6
- Uniform vs. adaptive sampling
What is a good mesh?
- Equal edge lengths
- Equilateral triangles
- Valence close to 6
- Uniform vs. adaptive sampling
- Feature preservation

What is a good mesh?
- Equal edge lengths
- Equilateral triangles
- Valence close to 6
- Uniform vs. adaptive sampling
- Feature preservation
- Alignment to curvature lines
- Isotropic vs. anisotropic
- Triangles vs. quadrilaterals
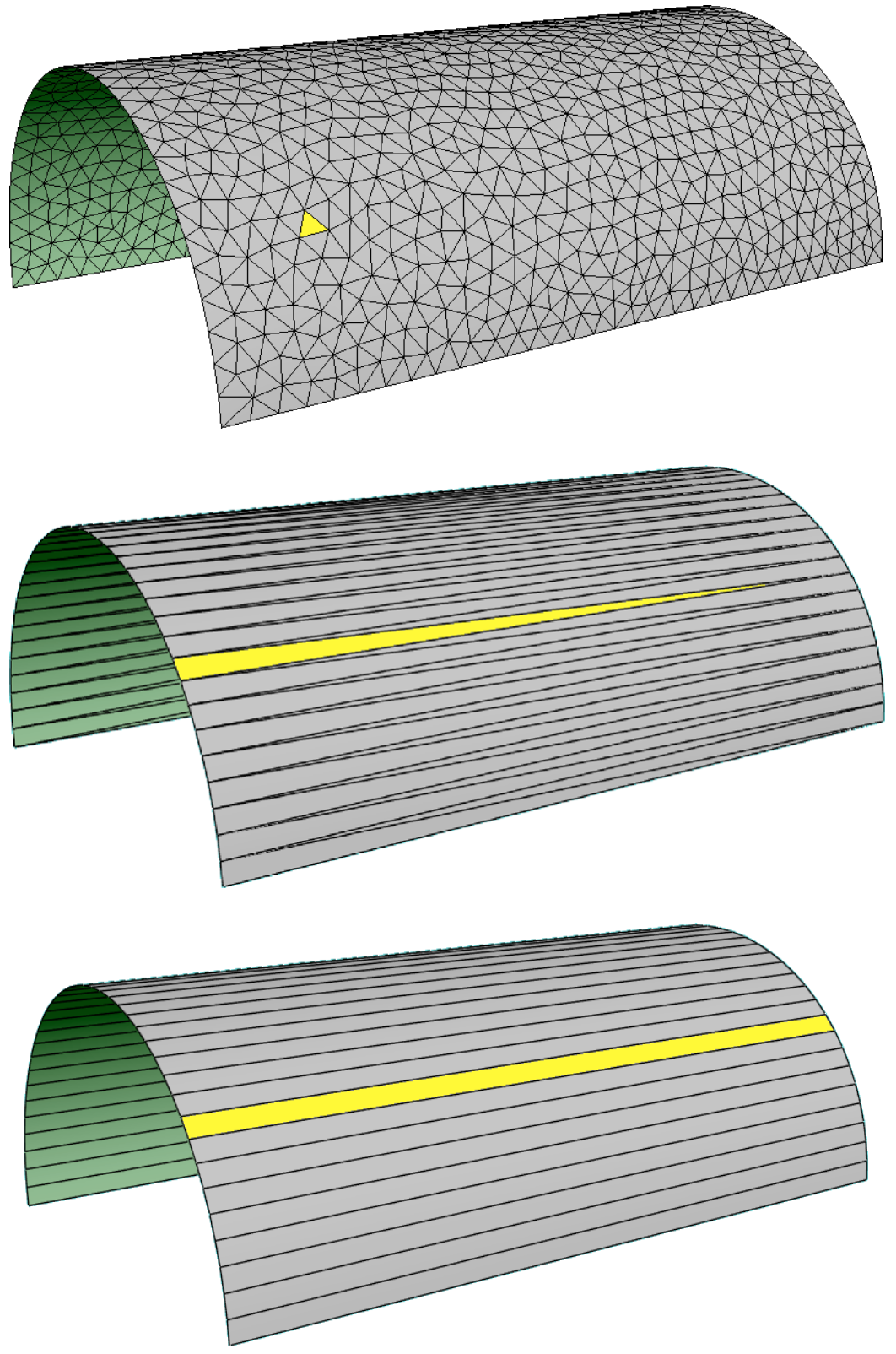
Isotropic Triangle Remeshing
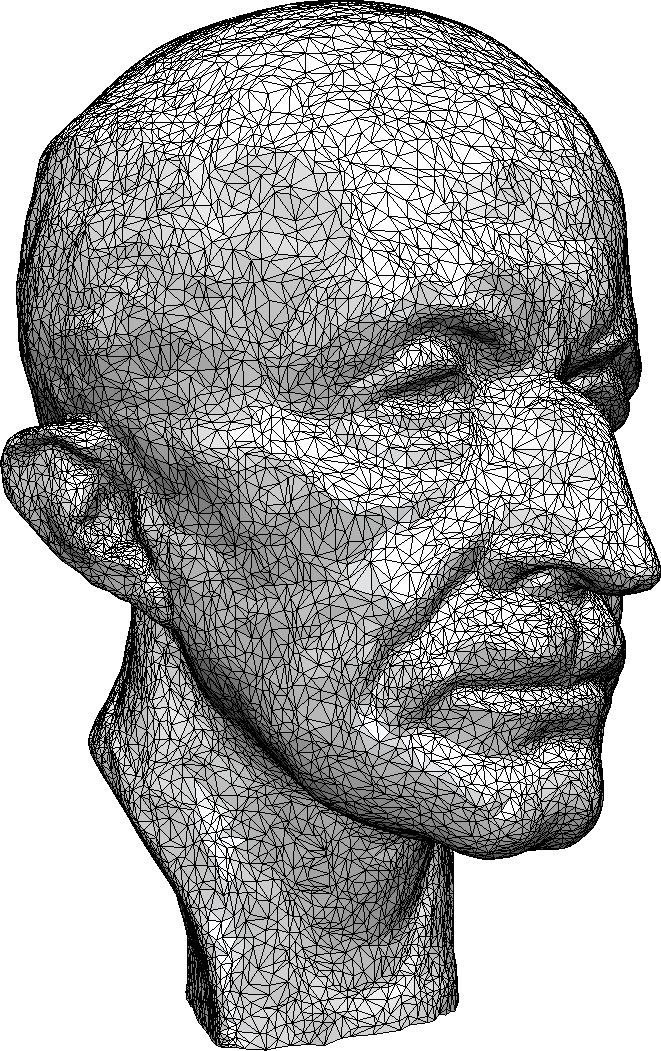
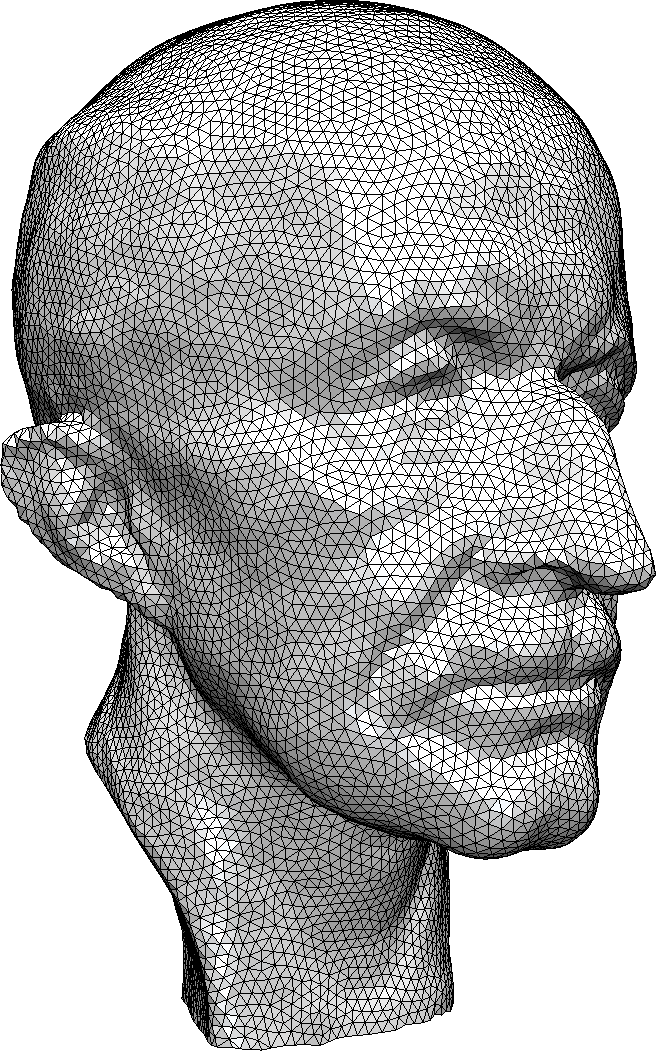

Local Remeshing Operators
- Edge collapse
- collapses two vertices of an edge into a single vertex
- is typically used to remove short edges
- removes one vertex, two triangles, three edges
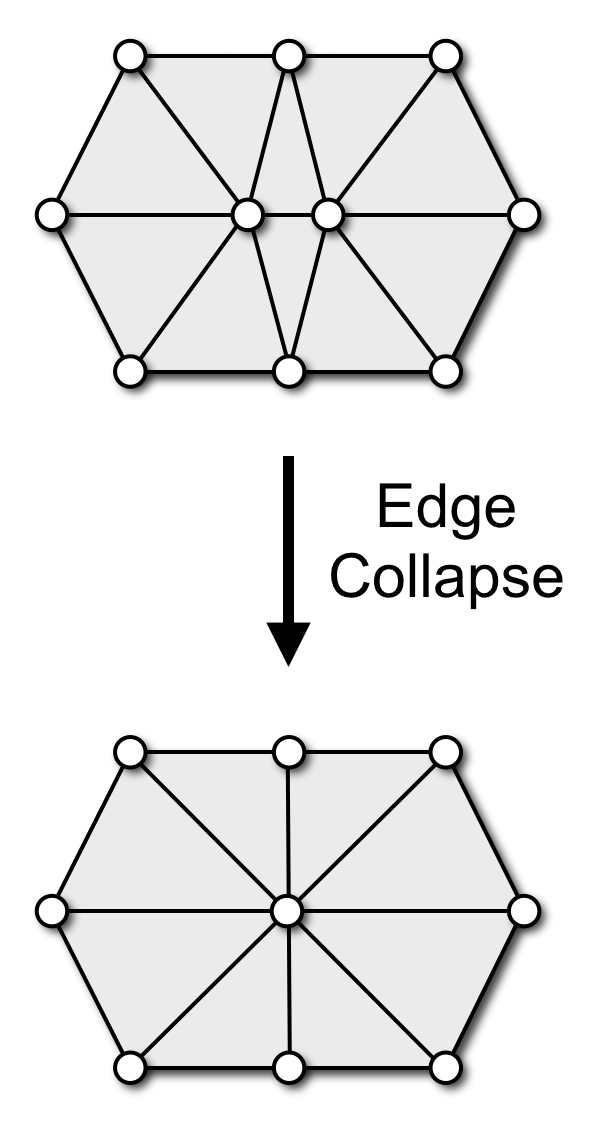
- Edge split
- splits an edge into two edges
- is typically used to remove long edges
- introduces one vertex, two triangles, three edges
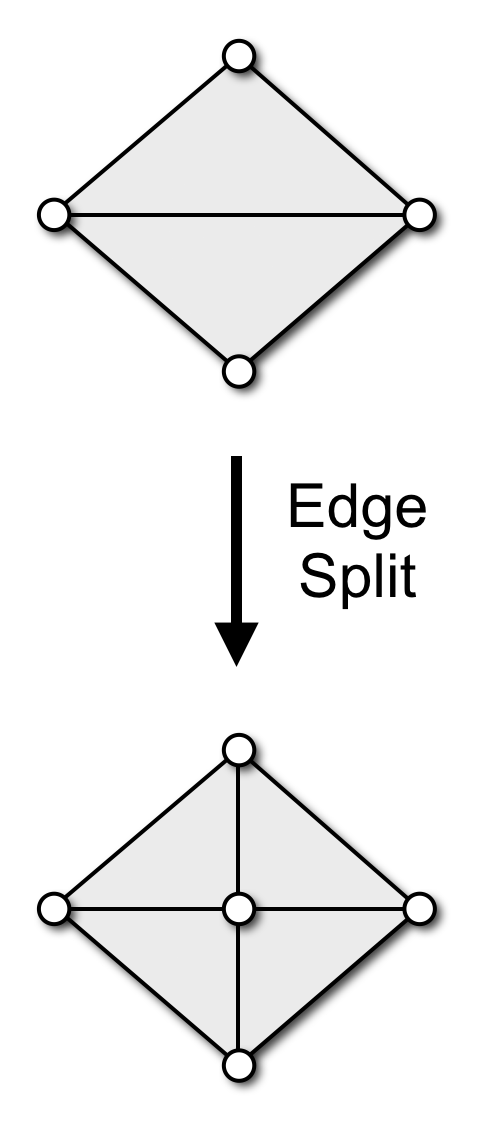
Local Remeshing Operators
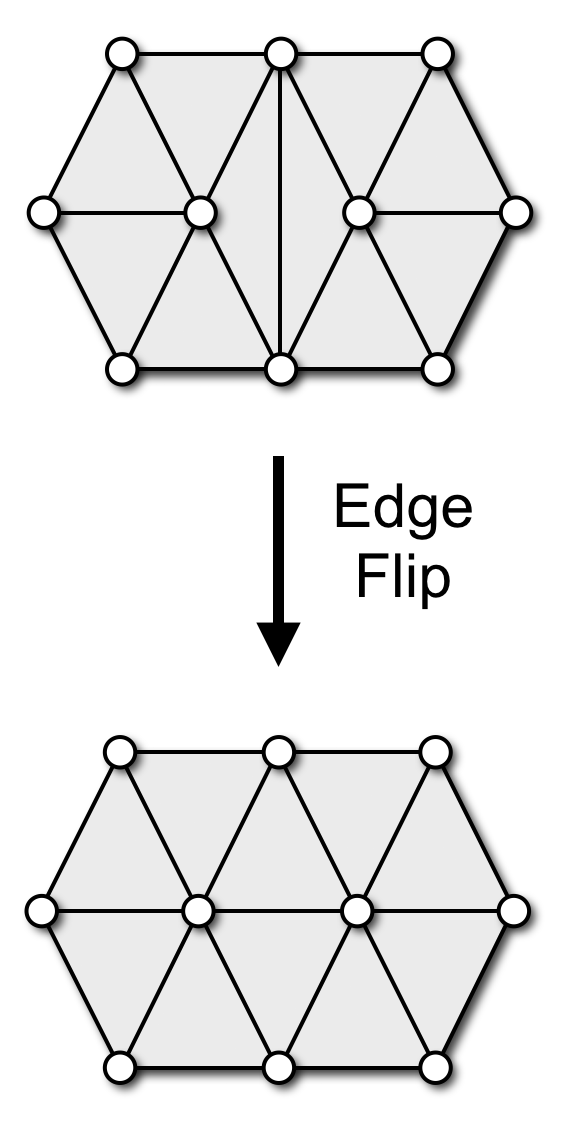
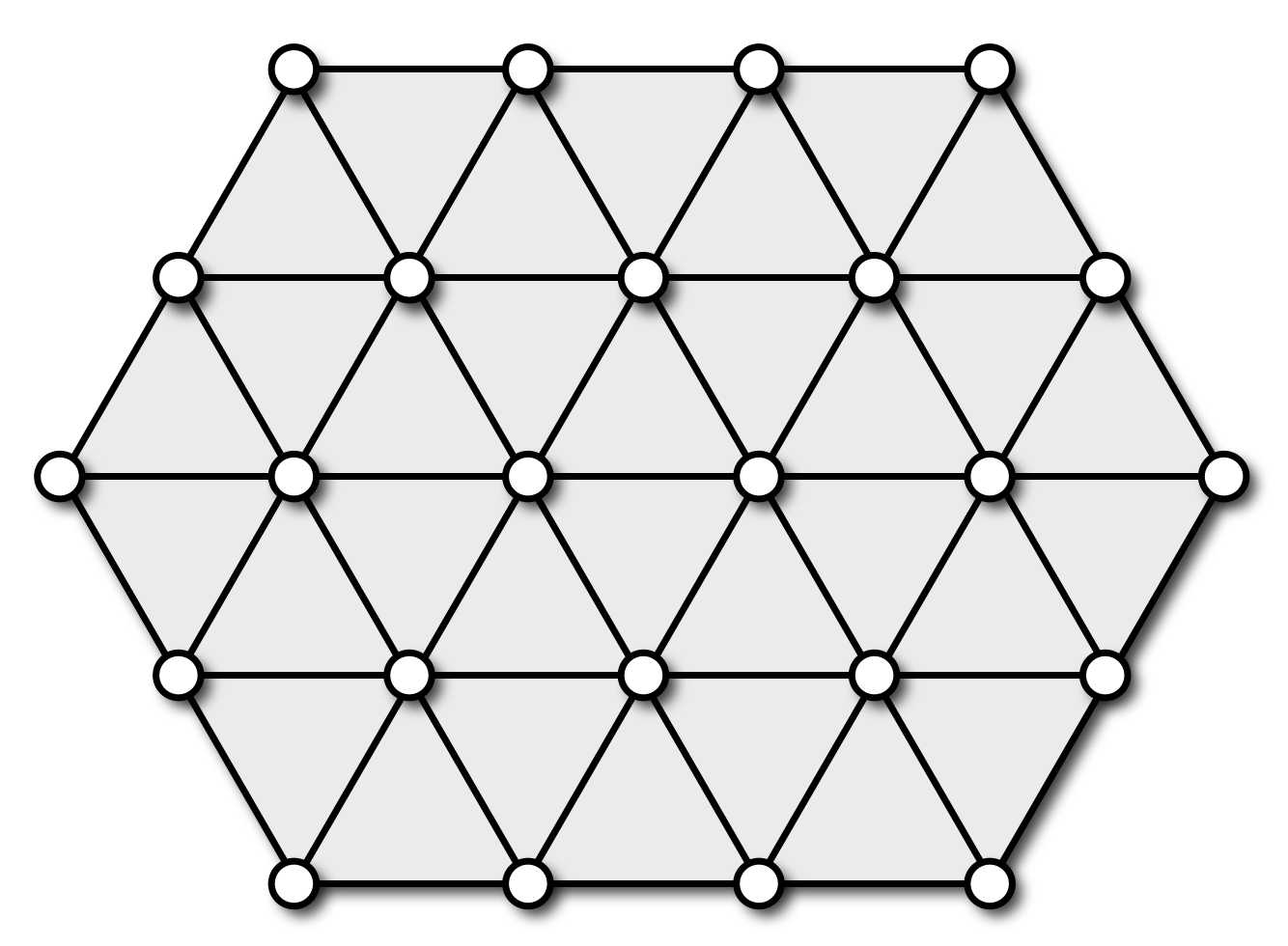
- Edge flip
- flip an edge incident to two triangles
- is typically used to balance the valence of vertices
- keeps the same number of vertices, edges, faces
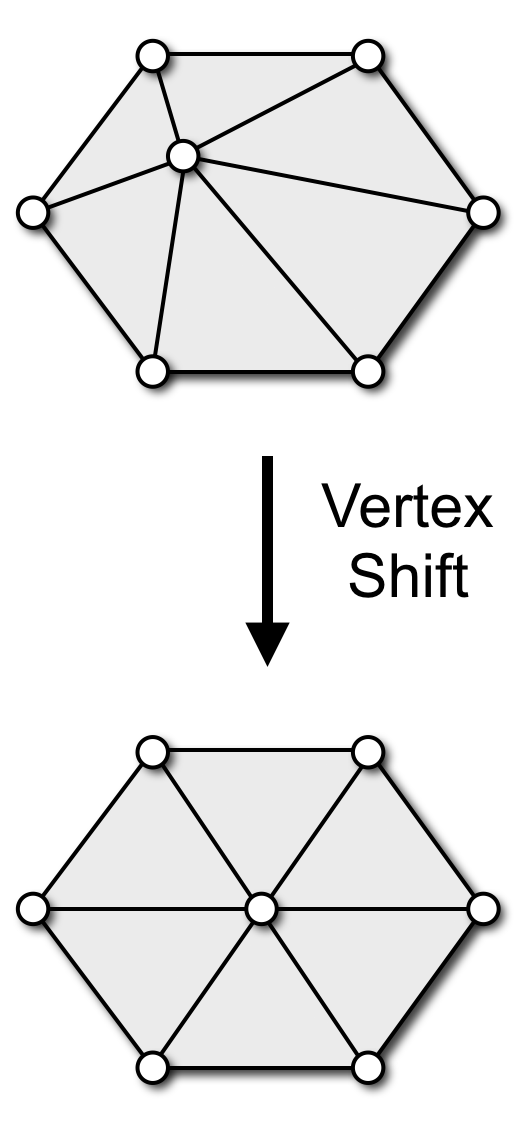
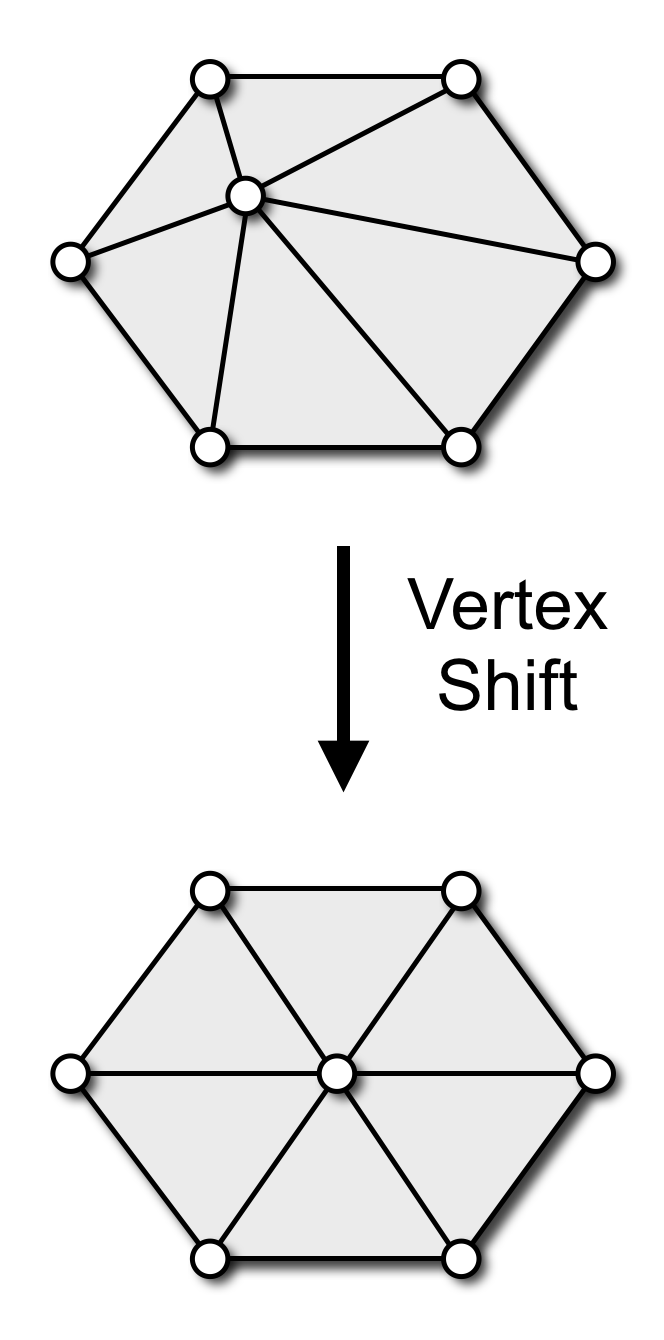
- Vertex shift
- moves single vertex
- is typically used to improve triangle quality
- can be implemented with uniform Laplacian smoothing
Local Remeshing Operators




Isotropic Remeshing
- Specify target edge length \(L\)
- Iterate
- Split edges longer than \(L_{\text{max}}\)
- Collapse edges shorter than \(L_{\text{min}}\)
- Flip edges to get closer to valence 6
- Shift vertices by tangential relaxation
- Project vertices onto input mesh
Edge Collapse / Split
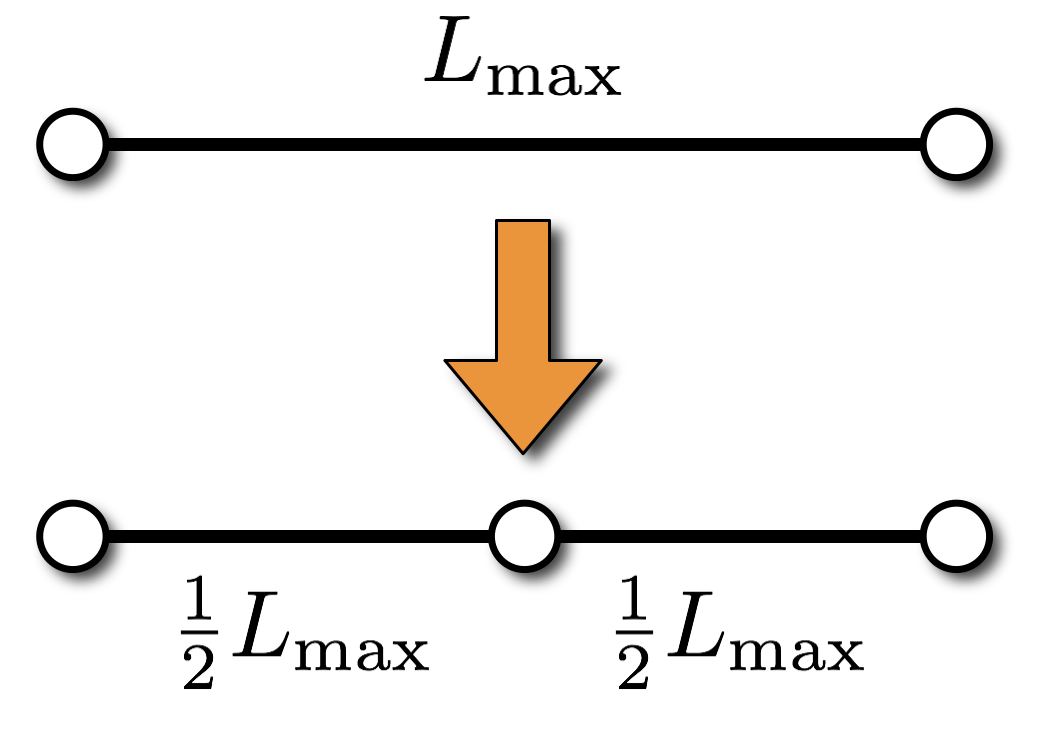
\[\begin{eqnarray*} \abs{L_{\max}-L} &=& \abs{\frac{1}{2}L_{\max}-L} \\ \Rightarrow L_{\max} &=& \frac{4}{3}L \end{eqnarray*}\]
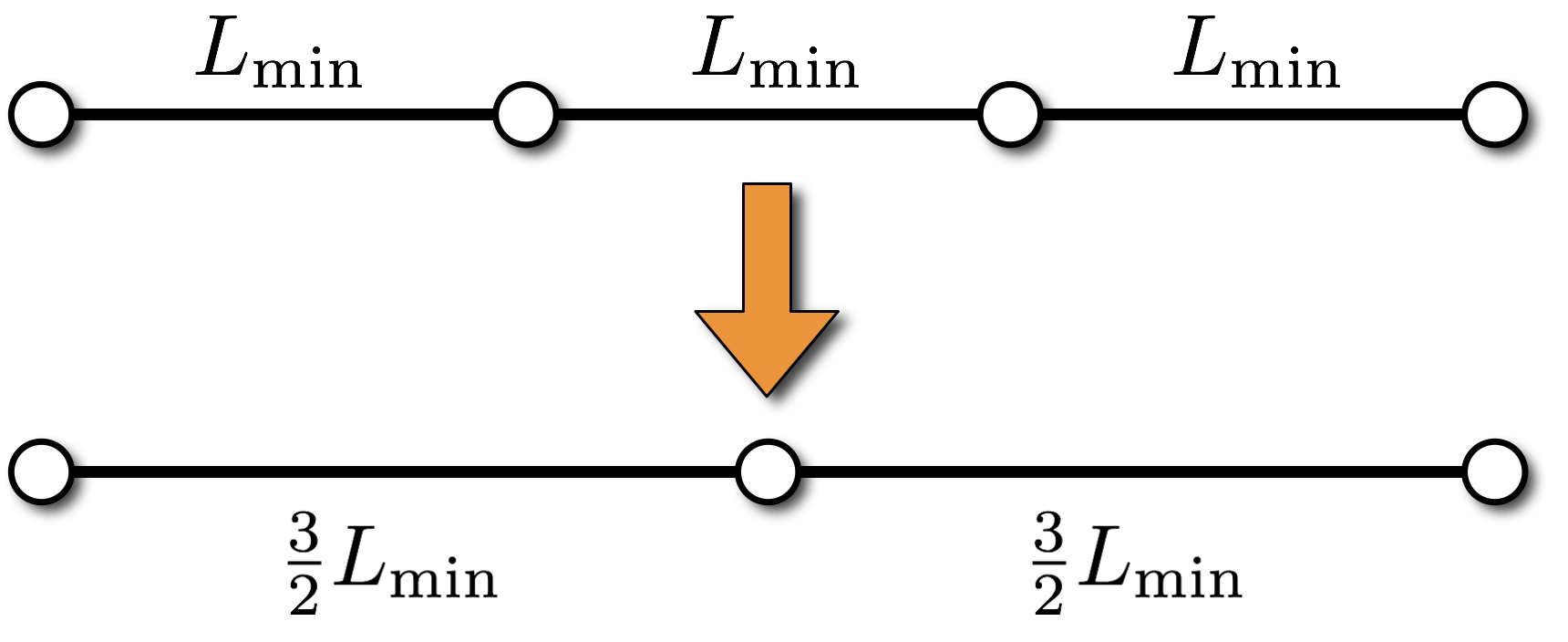
\[\begin{eqnarray*} \abs{L_{\min}-L} &=& \abs{\frac{3}{2}L_{\min}-L} \\ \Rightarrow L_{\min} &=& \frac{4}{5}L \end{eqnarray*} \]
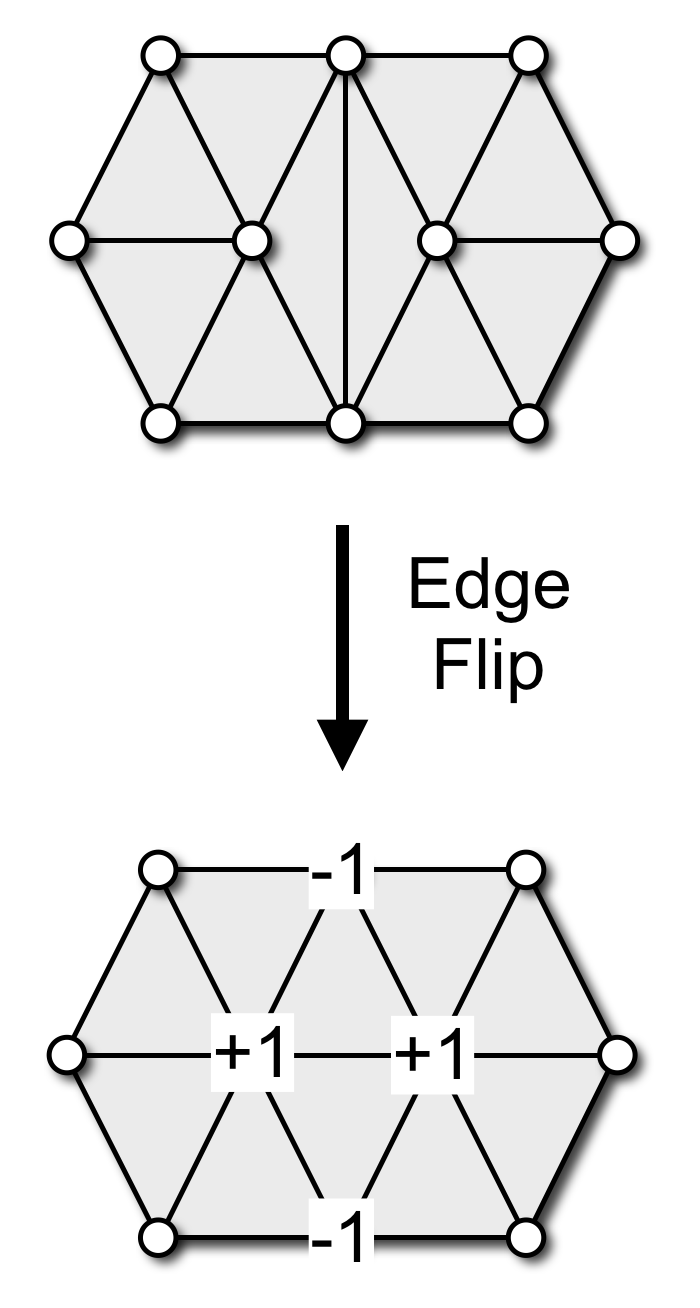
Edge Flip
- Improve valences
- Avg. valence is 6 (Euler)
- Reduce variation
- Optimal valence is
- 6 for interior vertices
- 4 for boundary vertices
Edge Flip
- Improve valences
- Avg. valence is 6 (Euler)
- Reduce variation
- Optimal valence is
- 6 for interior vertices
- 4 for boundary vertices
- Minimize valence excess \[\sum_{i=1}^4 \of{ \func{valence}\of{v_i} - \func{opt\_valence}\of{v_i} }^2\]
Vertex Shift
- Local “spring” relaxation
- Uniform Laplacian smoothing
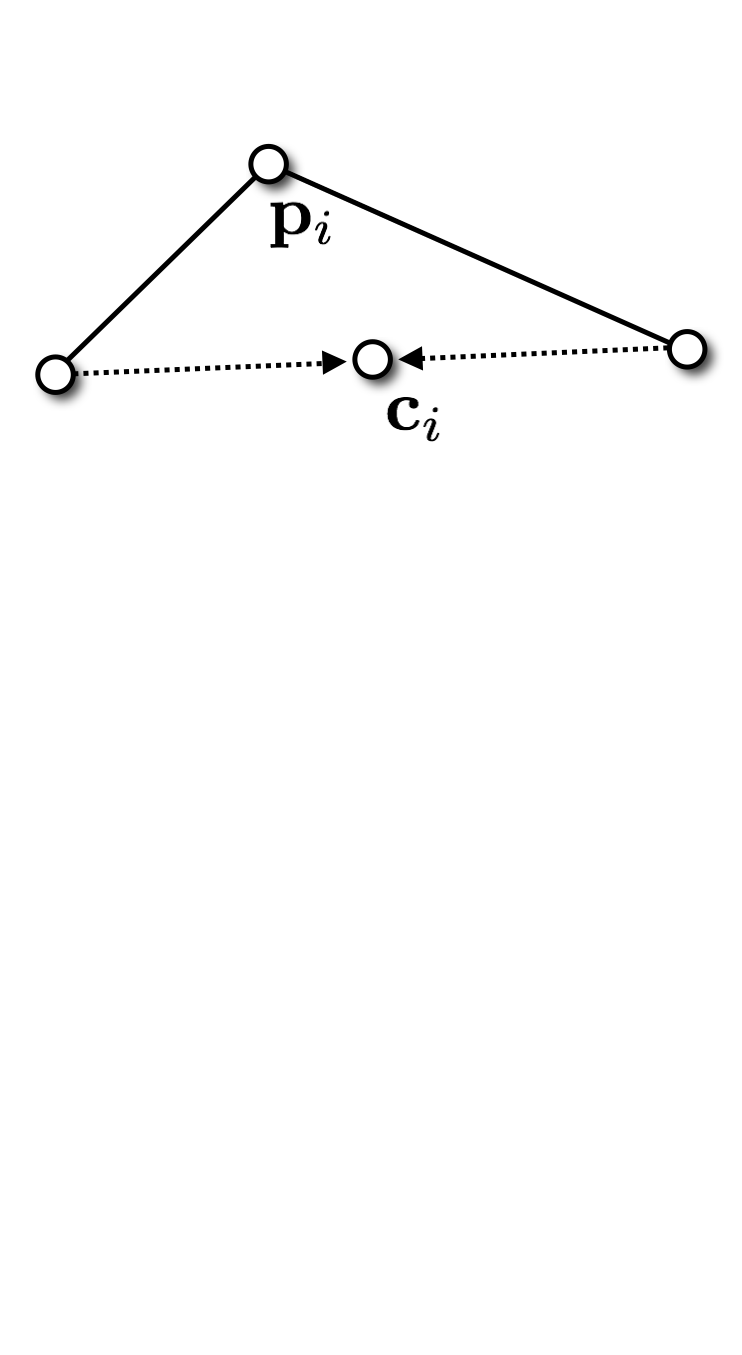
- Barycenter of one-ring neighbors
\[\vec{c}_i = \frac{1}{\func{valence}\of{v_i}} \sum_{j\in N\of{v_i}} \vec{p}_j\]
Vertex Shift
- Local “spring” relaxation
- Uniform Laplacian smoothing
- Barycenter of one-ring neighbors
\[\vec{c}_i = \frac{1}{\func{valence}\of{v_i}} \sum_{j\in N\of{v_i}} \vec{p}_j\]
Vertex Shift
- Local “spring” relaxation
- Uniform Laplacian smoothing
- Barycenter of one-ring neighbors
\[\vec{c}_i = \frac{1}{\func{valence}\of{v_i}} \sum_{j\in N\of{v_i}} \vec{p}_j\]
- Keep vertex (approx.) on surface
- Restrict movement to tangent plane
\[\vec{p}_i \leftarrow \vec{p}_i + \lambda \of{ \mat{I} - \vec{n}_i \vec{n}_i^T } \of{ \vec{c}_i - \vec{p}_i }\]
- Restrict movement to tangent plane
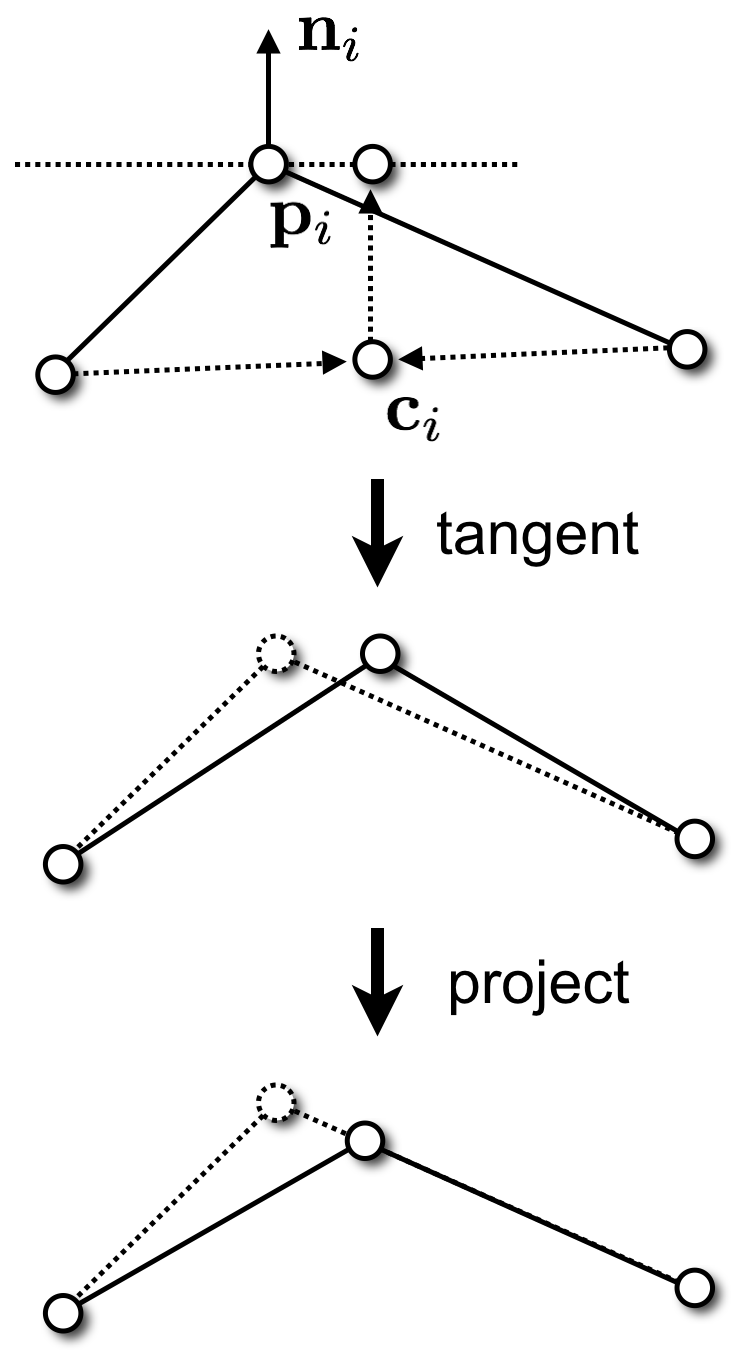
Isotropic Remeshing
- Specify target edge length \(L\)
- Iterate
- Split edges longer than \(L_{\text{max}}\)
- Collapse edges shorter than \(L_{\text{min}}\)
- Flip edges to get closer to valence 6
- Shift vertices by tangential relaxation
- Project vertices onto input mesh
Remeshing Results


Feature Preservation?
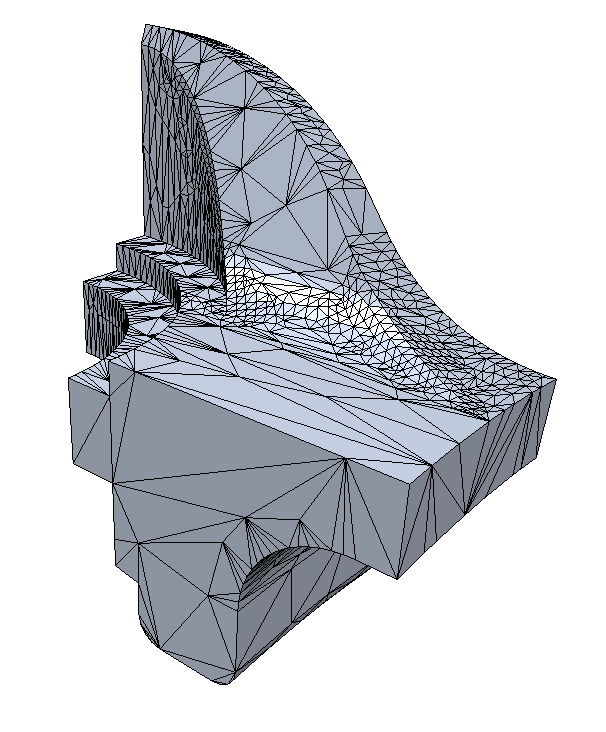

Feature Preservation
- Define feature edges / vertices
- Large dihedral angles
- Material boundaries
- Adjust local operators
- Don’t flip feature edges
- Collapse only along features
- Univariate smoothing
- Project to feature curves
- Don’t touch feature vertices

Adaptive Remeshing ?
- Adapt edge length to local curvature
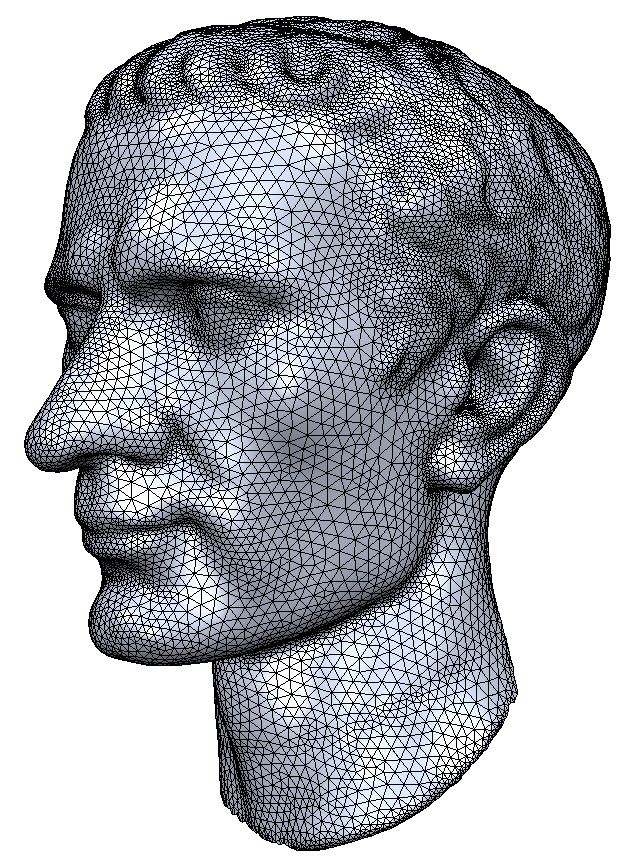
Adaptive Remeshing
- Adapt edge length to local curvature
- Compute maximum principle curvature on reference mesh
- Determine local target edge length from max-curvature
- Adjust split & collapse criteria accordingly

Let’s try!
Let’s try!
Real-Time Remeshing
Real-Time Remeshing
Literature
- Botsch et al., Polygon Mesh Processing, AK Peters, 2010
- Chapter 6.5.3: Remeshing
- Chapter 7.2: Decimation

