Lecture 3D Geometry Processing

Smoothing

Prof. Dr. David Bommes

Computer Graphics Group

Last week: Voronoi Diagram

Given a set of 2D sample points \(\{\mathbf{p}_1, \ldots , \mathbf{p}_n\}\)
Partition the plane by assigning each 2D point \(\mathbf{x}\) to its nearest sample.

All points assigned to \(\mathbf{p}_i\) form its Voronoi cell \[\mathcal{V}(\mathbf{p}_i) = \left\{ \mathbf{x} \in \mathbb{R}^2 : ||\mathbf{x}-\mathbf{p}_i|| \leq ||\mathbf{x}-\mathbf{p}_j|| \quad \forall j \neq i \right\}\]
Edges and vertices of these cells form the Voronoi diagram (VD).

Last week: Delaunay Triangulation

The dual graph of the Voronoi diagram is a planar straight line graph, the
Delaunay triangulation (DT)
- DT maximizes the minimum angle

Circumcircles of DT triangles are empty
- DT triangles are duals of VD vertices
- Criterion can be used for DT construction

Last week: Incremental Algorithm

For each point \(\mathbf{p}_i\)
- Find containing triangle
- Insert point into triangle (1-to-3 split)
- Flip edges to re-establish Delaunay property
Check whether an edge is Delaunay by testing circumcircles of its incident triangles
- Flip edge to make it Delaunay

Last week: Centroidal Voronoi Diagrams

Smoothing

Motivation

Filter out high-frequency noise

Motivation

Filter out high-frequency noise

Desbrun et al.: Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

Motivation

Advanced filtering

Kim, Rosignac: Geofilter: Geometric Selection of Mesh Filter Parameters, Eurographics 2005

Outline

Motivation
Spectral Analysis
Diffusion Equation
Numerical Solutions

Fourier Transform

Represent a function as a weighted sum of sine and cosine functions

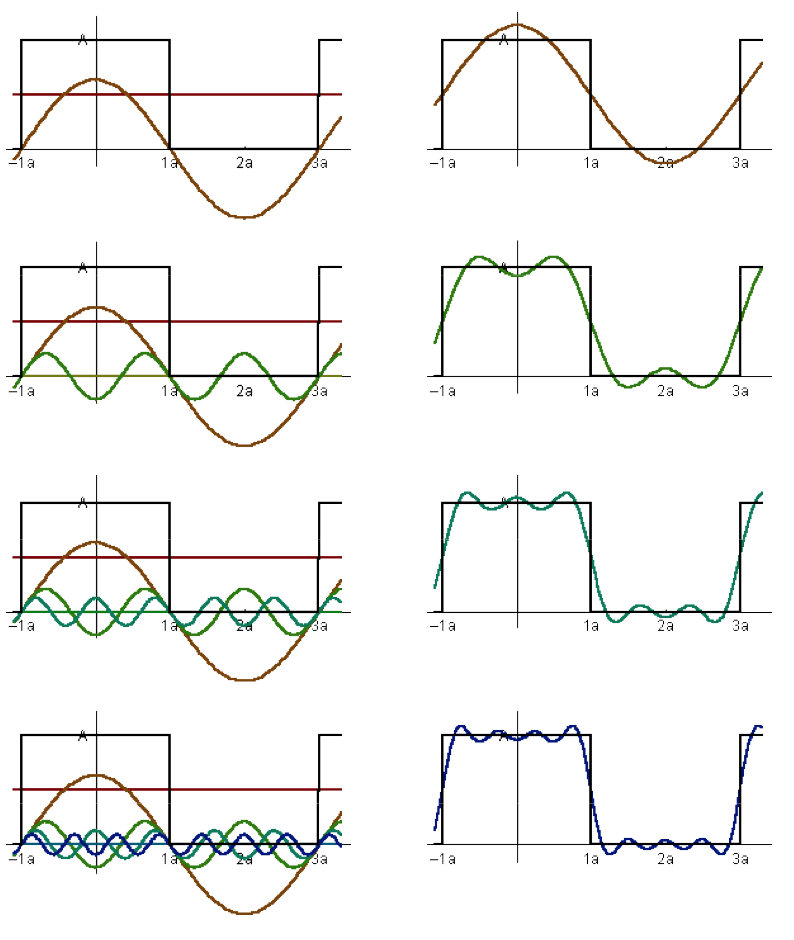
\[ f\of{x} \;=\; a_0 + a_1 \cos\of{x} + a_2 \cos\of{3x} + a_3 \cos\of{5x} + a_4 \cos\of{7x} + \dots \]

Fourier Transform

\[F(\omega) = \int_{-\infty}^{\infty} f(x) \, \func{e}^{-2\pi\func{i}\omega x} \func{d}x\]

\[f(x) = \int_{-\infty}^{\infty} F(\omega) \, \func{e}^{2\pi\func{i}\omega x} \;\func{d}\omega\]

Wikipedia: Fourier Transform and \(L^2\) Inner Product

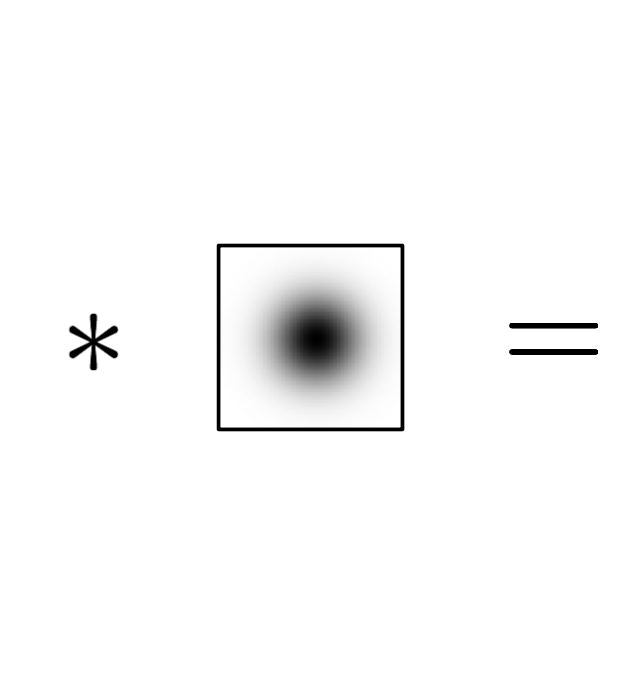
Convolution

Smooth signal by convolution with a kernel function \[ h(x) \;=\; f * g \;:=\; \int f(y) \cdot g(x-y) \,\func{d}y \]
Example: Gaussian blurring

Wikipedia: Convolution

Convolution

Smooth signal by convolution with a kernel function \[ h(x) \;=\; f * g \;:=\; \int f(y) \cdot g(x-y) \,\func{d}y \]
Convolution in spatial domain ⇔ Multiplication in frequency domain \[ H\of{\omega} \;=\; F\of{\omega} \cdot G\of{\omega} \]

Filtering with Fourier Transform

Spatial domain \(f(x) \rightarrow\) frequency domain \(F(\omega)\)
\[ F(\omega) = \int_{-\infty}^{\infty} f(x) \, \func{e}^{-2\pi \func{i}\omega x} dx\]
Multiply by low-pass filter \(G(\omega)\)
\[ F(\omega) \leftarrow F(\omega) G(\omega)\]
Frequency domain \(F(\omega) \rightarrow\) spatial domain \(f(x)\)
\[ f(x) = \int_{-\infty}^{\infty} F(\omega) \, \func{e}^{2\pi \func{i}\omega x} dx\]

Filtering with Fourier Transform

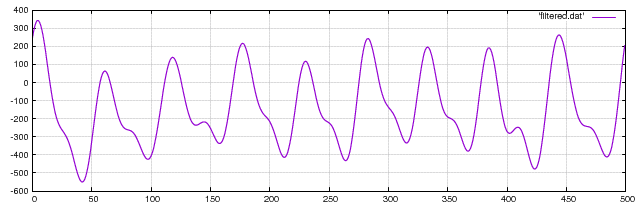
Filtering with Fourier Transform

Spectral Analysis for Meshes

Fourier transform requires functional representation
How to generalize to meshes?
Observation: Complex waves are eigenfunctions of Laplacian \[\Delta e^{2 \pi i \omega x} = \frac{\func{d}^2}{\func{d}x^2} \func{e}^{2 \pi \func{i} \omega x} = -(2 \pi \omega)^2 \func{e}^{2 \pi \func{i} \omega x}\]
Idea: Use eigenfunctions of discrete Laplace-Beltrami operator as spectral basis

Wikipedia: Eigenfunctions

Discrete Laplace-Beltrami

Function values sampled at mesh vertices \[\vec{f} = [f_1, f_2, \ldots, f_n] \in \R^n\]
Discrete Laplace-Beltrami (per vertex) \[ \laplace_{\set{S}} f\of{v_i} := \frac{1}{2A_i} \sum_{v_j \in \set{N}_1\of{v_i}} \left( \func{cot} \alpha_{ij} + \func{cot} \beta_{ij} \right) \left( f \of{v_j} - f \of{v_i} \right)\]

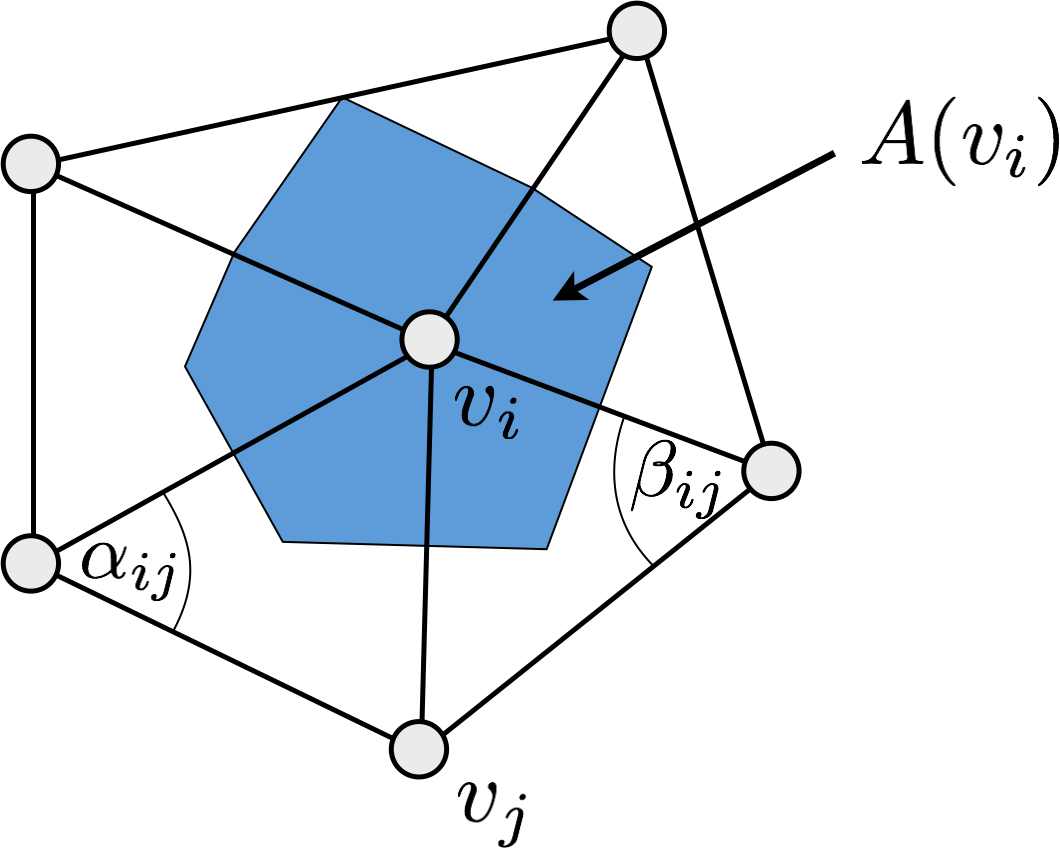
Discrete Laplace-Beltrami

Discrete Laplace operator (per mesh)
- Sparse matrix \(\mat{L} = \mat{DM} \in \R^{n \times n}\)

\[ \matrix{\vdots \\ \laplace_\set{S} f\of{v_i} \\ \vdots} \;=\; \mat{L} \cdot \matrix{\vdots \\ f \of{v_i} \\ \vdots} \]

Discrete Laplace-Beltrami

Discrete Laplace operator (per mesh)
- Sparse matrix \(\mat{L} = \mat{DM} \in \R^{n \times n}\)

\[ \mat{M}_{ij} \;=\; \begin{cases} \func{cot}\alpha_{ij} + \func{cot}\beta_{ij}, & i \ne j \,,\; j \in \set{N}_1\of{v_i} \\ - \sum_{v_j \in \set{N}_1 \of{v_i}}\of{ \func{cot}\alpha_{ij} + \func{cot}\beta_{ij} } & i=j \\ 0 & \text{otherwise} \end{cases} \]

\[\mat{D} = \func{diag}\of{ \dots, \frac{1}{2A_i}, \dots}\]

Spectral Mesh Analysis

Discrete Laplace-Beltrami matrix \(\vec{L}\)
- Eigenvectors are “natural vibrations”
- Eigenvalues are “natural frequencies”

Levy, Zhang: Spectral Mesh Processing, SIGGRAPH Courses 2010

Spectral Mesh Analysis

Setup Laplace-Beltrami matrix \(\vec{L}\)
Compute \(k\) smallest eigenvectors \(\{\vec{e}_1, \ldots, \vec{e}_k\}\)
Reconstruct mesh from those (component-wise)

\[\begin{eqnarray} \vec{x} &:=& \left[ x_1, \dots, x_n \right] \\ \vec{x} &\leftarrow& \sum_{i=1}^k \, \left( \trans{\vec{x}} \vec{e}_i \right) \vec{e}_i \end{eqnarray}\]

\[\begin{eqnarray} \vec{y} &:=& \left[ y_1, \dots, y_n \right] \\ \vec{y} &\leftarrow& \sum_{i=1}^k \, \left( \trans{\vec{y}} \vec{e}_i \right) \vec{e}_i \end{eqnarray}\]

\[\begin{eqnarray} \vec{z} &:=& \left[ z_1, \dots, z_n \right] \\ \vec{z} &\leftarrow& \sum_{i=1}^k \, \left( \trans{\vec{z}} \vec{e}_i \right) \vec{e}_i \end{eqnarray}\]

Math Background: Inner Product

Spectral Mesh Analysis

Setup Laplace-Beltrami matrix \(\vec{L}\)
Compute \(k\) smallest eigenvectors \(\{\vec{e}_1, \ldots, \vec{e}_k\}\)
Reconstruct mesh from those (component-wise)

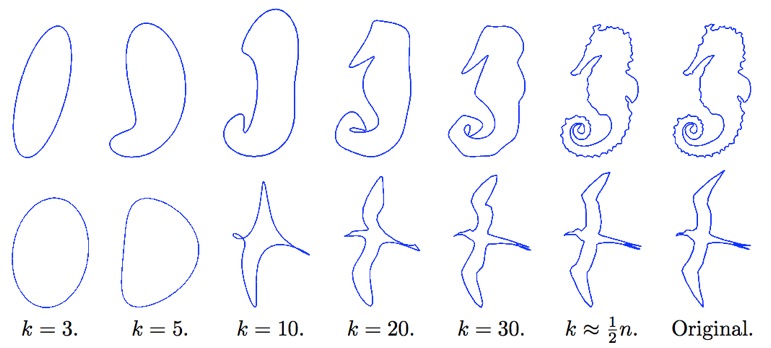
Levy, Zhang: Spectral Mesh Processing, SIGGRAPH Courses 2010

Spectral Mesh Analysis

Setup Laplace-Beltrami matrix \(\vec{L}\)
Compute \(k\) smallest eigenvectors \(\{\vec{e}_1, \ldots, \vec{e}_k\}\)
Reconstruct mesh from those (component-wise)

Levy, Zhang: Spectral Mesh Processing, SIGGRAPH Courses 2010

Too complex for large meshes!

Outline

Motivation
Spectral Analysis
Diffusion Equation
Numerical Solutions

Diffusion Flow

Diffusion equation

\[\frac{\partial f}{\partial t} = \lambda \Delta f\]
- \(\lambda\) is the diffusion constant
- \(\Delta\) is the Laplace operator

Wikipedia: Diffusion Equation

Diffusion Flow

2nd order elliptic PDE

\[\frac{\partial f(x,y,t)}{\partial t} \;=\; \lambda \left( \frac{\partial^2 f(x,y,t)}{\partial x^2} + \frac{\partial^2 f(x,y,t)}{\partial y^2} \right)\]
Solve numerically
- Discretize in space & time
- Discretize time derivative
- Discretize spatial derivatives

Discretize in Space & Time

Sample function \(f(x,y,t)\) on a regular grid with grid spacing \(h\) and time step \(\delta_t\) \[f[i,j,t] \;=\; f\left(i \cdot h, j \cdot h, t \cdot \delta t \right) \] \[i=1, \dots, n \quad j=1, \dots, m \quad t=0, 1, 2, \dots\]

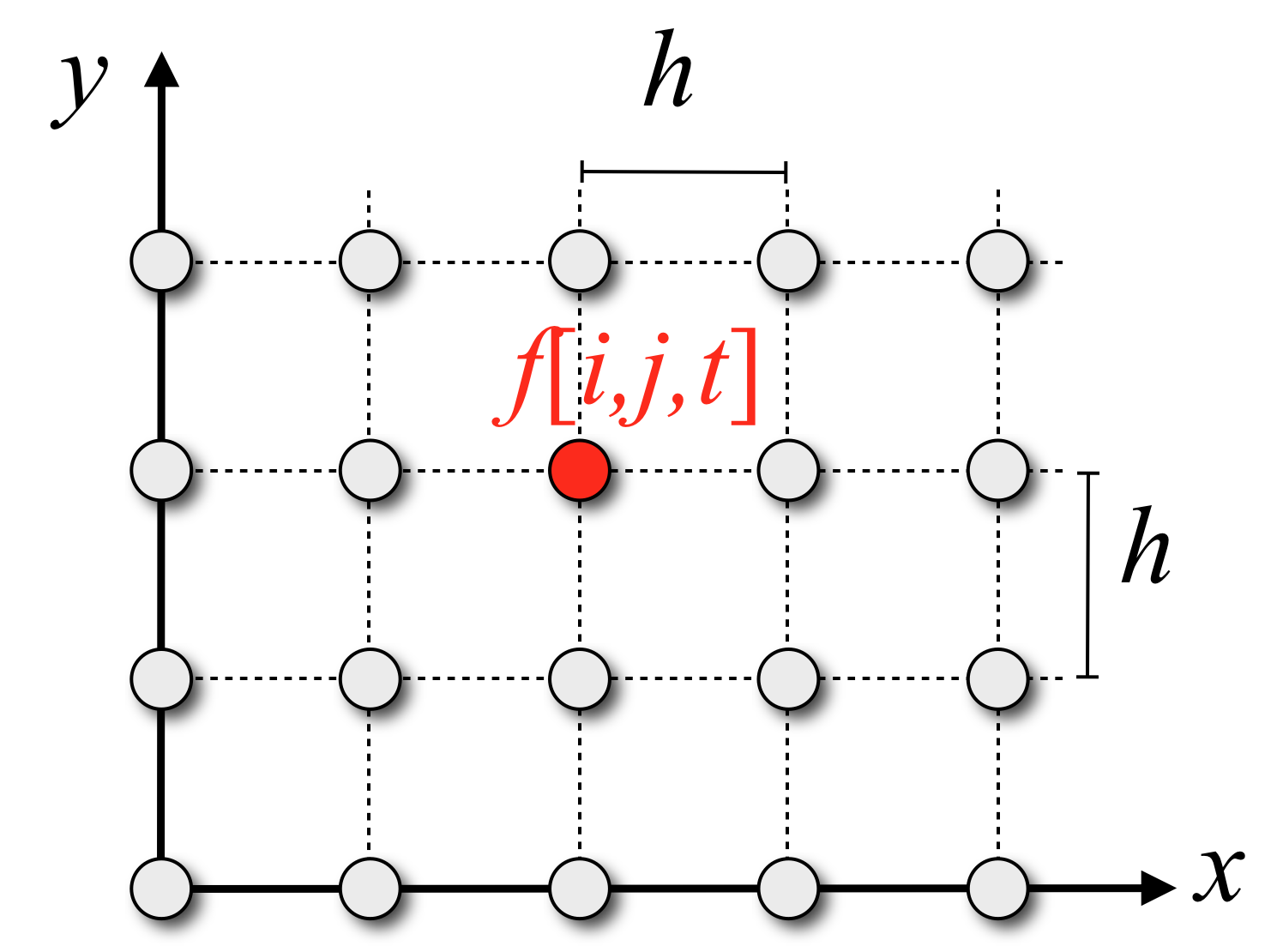
Finite Differences

Approximate \(f(x+h)\) from Taylor series \[ \begin{align} f(x+h) &\;=\; f(x) + h f'(x) + \frac{h^2}{2!} f''(x) + \ldots \\ &\;\approx\; f(x) + h f’(x) \end{align}\]

Approximate \(f'(x)\) as \[f'(x) \;\approx\; \frac{f(x+h) - f(x)}{h}\]

Finite Difference Method

Approximation of spatial derivatives

\[ \begin{align} f_{,x}[i,j,t] &\;\approx\; \frac{f[i+1,j,t] - f[i,j,t]}{h} &\text{forward difference} \\[2mm] f_{,x}[i,j,t] &\;\approx\; \frac{f[i,j,t] - f[i-1,j,t]}{h} &\text{backward difference} \\[2mm] f_{,x}[i,j,t] &\;\approx\; \frac{f[i+1,j,t] - f[i-1,j,t]}{2h} &\text{central difference} \end{align} \]

Finite Difference Method

Approximation of higher-order derivatives

\[ \begin{align} f_{,xx}[i,j,t] &\;\approx\; \frac{f_{,x}[i,j,t] - f_{,x}[i-1,j,t]}{h} \\[2mm] &\;=\; \frac{f[i+1,j,t] -2f[i,j,t] + f[i-1,j,t]}{h^2} \end{align} \]
Approximation of Laplacian

\[ \begin{align} \laplace f[i,j,t] &\;\approx\; f_{,xx}[i,j,t] + f_{,yy}[i,j,t] \\[2mm] &\;=\; \frac{f[i+1,j,t] + f[i-1,j,t] + f[i,j+1,t] + f[i,j-1,t] - 4f[i,j,t] }{h^2} \end{align} \]

Finite Difference Method

Approximation of temporal derivative

\[ f_{,t}[i,j,t] \;\approx\; \frac{f[i,j,t+1] - f[i,j,t]}{\delta t}\]

Leads to explicit Euler integration

\[ f[i,j,t+1] \;\approx\; f[i,j,t] + \delta t \cdot f_{,t}[i,j,t]\]

Diffusion Flow

Continuous PDE \[\frac{\partial f(x,y,t)}{\partial t} \;=\; \lambda \left( \frac{\partial^2 f(x,y,t)}{\partial x^2} + \frac{\partial^2 f(x,y,t)}{\partial y^2} \right)\]

Finite difference discretization \[\frac{f[i,j,t+1] - f[i,j,t]}{\delta t} \;=\; \lambda \frac{f[i+1,j,t] + f[i-1,j,t] + f[i,j+1,t] + f[i,j-1,t] - 4f[i,j,t] }{h^2}\] \[f[i,j,t+1] \;=\; f[i,j,t] + \delta t \lambda \frac{f[i+1,j,t] + f[i-1,j,t] + f[i,j+1,t] + f[i,j-1,t] - 4f[i,j,t] }{h^2}\]

\(\frac{\delta t \lambda}{h^2}\) has to be small
( \(\leq 1\) in this case)

Diffusion in 2D

Diffusion Flow on Meshes

Continuous PDE: \(\frac{\partial \vec{p}}{\partial t} \;=\; \lambda \Delta \vec{p}\)
Discretization: \(\vec{p}_i \leftarrow \vec{p}_i + \delta t \, \lambda \Delta \vec{p}_i\)

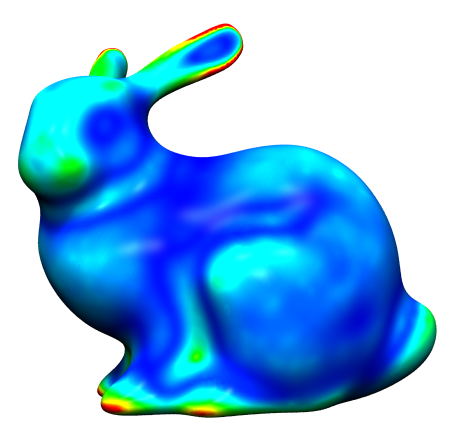
Diffusion Flow on Meshes

Problem: Time step needs to be very small to give stable results when using cotan Laplacian with area normalization
Better results with normalized weights
(and ignoring the area term) \[\laplace \vec{p}_i \;=\; \frac{1}{\sum_{v_j \in \set{N}_1\of{v_i}} w_{ij}} \sum_{v_j \in \set{N}_1\of{v_i}} w_{ij} \left( \vec{p}_j - \vec{p}_i \right) \]
- Uniform weights \(w_{ij} = 1\)
- Cotangent weights \(w_{ij} = \cot\alpha_{ij} + \cot\beta_{ij}\)

Uniform Laplace Discretization

Smoothes geometry and triangulation
Can be non-zero even for planar triangulations
Vertex drift can lead to distortions
Might be desired for mesh regularization

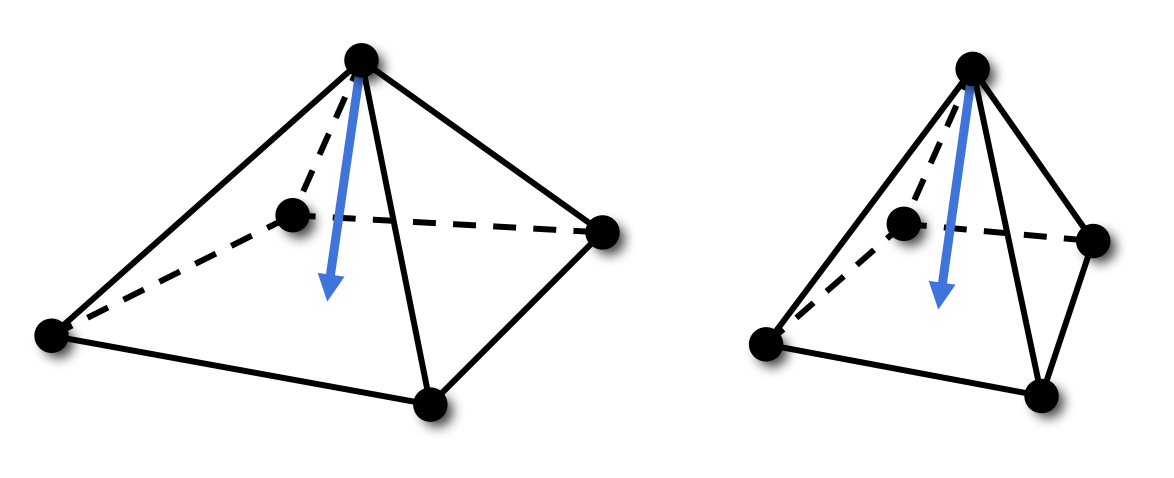
Desbrun et al.: Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

Uniform vs Cotan Discretization

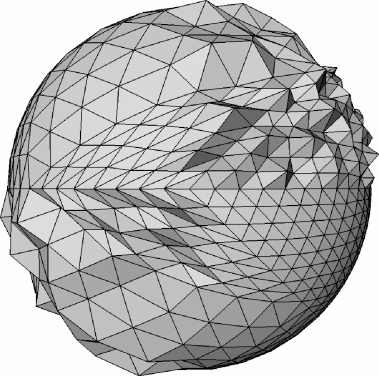
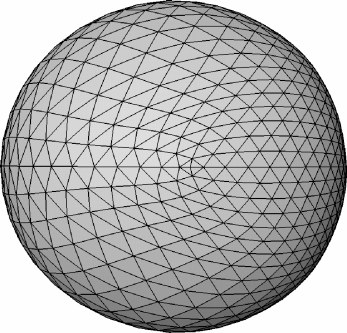
Outline

Motivation
Spectral Analysis
Diffusion Equation
Numerical Solutions

Numerical Integration

Let’s write the position update in matrix notation
Write all points \(\vec{p}_i^{(t)}\) in a large vector/matrix: \[\vec{P}^{(t)} = \trans{\left( \vec{p}_1^{(t)}, \ldots, \vec{p}_n^{(t)} \right)} \in \R^{n\times 3}\]
Matrix version of explicit integration \[\vec{P}^{(t+1)} = (\vec{I} + \delta t \, \lambda \vec{L}) \, \vec{P}^{(t)}\]
Matrix version of implicit integration \[(\vec{I} - \delta t \, \lambda \vec{L}) \, \vec{P}^{(t+1)} = \vec{P}^{(t)}\]

requires small \(\delta t \lambda\) for stability!

works for any \(\delta t \lambda\)!

Wikipedia: Explicit/Implicit Integration

How to solve the linear system?

Solve linear system in each iteration \[(\vec{I} - \delta t \, \lambda \vec{L}) \vec{P}^{(t+1)} = \vec{P}^{(t)}\]

Matrix \(\vec{L} = \vec{DM}\) is built from Laplace weights \[\mat{M}_{ij} \;=\; \begin{cases} \func{cot}\alpha_{ij} + \func{cot}\beta_{ij}, & i \ne j \,,\; j \in \set{N}_1\of{v_i} \\ - \sum_{v_j \in \set{N}_1 \of{v_i}}\of{ \func{cot}\alpha_{ij} + \func{cot}\beta_{ij} } & i=j \\ 0 & \text{otherwise} \end{cases} \]

\[\mat{D} = \func{diag}\of{ \dots, \frac{1}{2A_i}, \dots}\]

How to solve the linear system?

Solve linear system in each iteration \[(\vec{I} - \delta t \, \lambda \vec{L}) \vec{P}^{(t+1)} = \vec{P}^{(t)}\]

Which solvers do you know?
- Gaussian elimination? 💣
- LU factorization? 💣

Analyze the properties of your system matrix!
- very sparse (about 7 non-zeros per row) 😄
- but not symmetric 😢

How to solve the linear system?

Matrix \(\vec{L} = \vec{DM}\) is not symmetric because of \(\vec{D}\).
Symmetrize it by multiplying with \(\vec{D}^{-1}\) from the left \[(\vec{D}^{-1} - \delta t \, \lambda \vec{M}) \vec{P}^{(t+1)} = \vec{D}^{-1} \vec{P}^{(t)}\]
Now the linear system is
- sparse 😄
- symmetric 😄
- positive definite 😄
We can use much more efficient solvers!
- conjugate gradients 😘
- sparse Cholesky factorization 😍

Try it yourself!

Literature

Botsch et al., Polygon Mesh Processing, AK Peters, 2010
- Chapter 4

Taubin, A Signal Processing Approach to Fair Surface Design, SIGGRAPH 1995
Desbrun, Meyer, Schröder, Barr: Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

Literature

Botsch et al., Polygon Mesh Processing, AK Peters, 2010
- Chapter 4

Taubin, A Signal Processing Approach to Fair Surface Design, SIGGRAPH 1995
Desbrun, Meyer, Schröder, Barr: Implicit Fairing of Irregular Meshes using Diffusion and Curvature Flow, SIGGRAPH 1999

Last week: Voronoi Diagram

Last week: Delaunay Triangulation

Last week: Incremental Algorithm

Last week: Delaunay Refinement

Last week: Centroidal Voronoi Diagrams

Smoothing

Motivation

Motivation

Motivation

Outline

Fourier Transform

Fourier Transform

Convolution

Convolution

Filtering with Fourier Transform

Filtering with Fourier Transform

Filtering with Fourier Transform

Spectral Analysis for Meshes

Discrete Laplace-Beltrami

Discrete Laplace-Beltrami

Discrete Laplace-Beltrami

Spectral Mesh Analysis

Spectral Mesh Analysis

Spectral Mesh Analysis

Spectral Mesh Analysis

Outline

Diffusion Flow

Diffusion Flow

Discretize in Space & Time

Finite Differences

Finite Difference Method

Finite Difference Method

Finite Difference Method

Diffusion Flow

Diffusion in 2D

Diffusion Flow on Meshes

Diffusion Flow on Meshes

Uniform Laplace Discretization

Uniform vs Cotan Discretization

Outline

Numerical Integration

How to solve the linear system?

How to solve the linear system?

How to solve the linear system?

Try it yourself!

Try it yourself!

Try it yourself!

Try it yourself!

Literature

Literature