Surface Reconstruction
- Goal: Transform acquired samples into triangle mesh




Surface Reconstruction
Goal: Transform acquired samples into triangle mesh
Main Approach:
- First reconstruct an implicit function
- Then extract isosurface using Marching Cubes (MC)





- Advantages
- result is closed 2-manifold surface
- suitable for noisy input data
Recall: 2D Marching Squares Algorithm
- Classify grid nodes as inside/outside
- Is \(F(x_{i,j})\) below or above iso-value?
- Classify cell: \(2^4 = 16\) configurations
- in/out for each corner
- Determine contour edges
- look-up table for edge configuration
- Determine vertex positions
- linear interpolation of grid values along edges
Recall: 2D Marching Squares Algorithm
3D Marching Cubes Algorithm
- Classify grid nodes as inside/outside
- Is \(F(x_{i,j,k})\) below or above iso-value?
- Classify cell: \(2^8 = 256\) configurations
- in/out for each corner
- Determine contour triangles
- look-up table for triangle configuration
- Determine vertex positions
- linear interpolation of grid values along edges
3D Marching Cubes Algorithm
- Cell Configurations
Poisson Surface Reconstruction
- Slides courtesy of Misha Kazhdan
- Source Code available at:
- http://www.cs.jhu.edu/~misha/
- Implementation included in Meshlab and many other tools

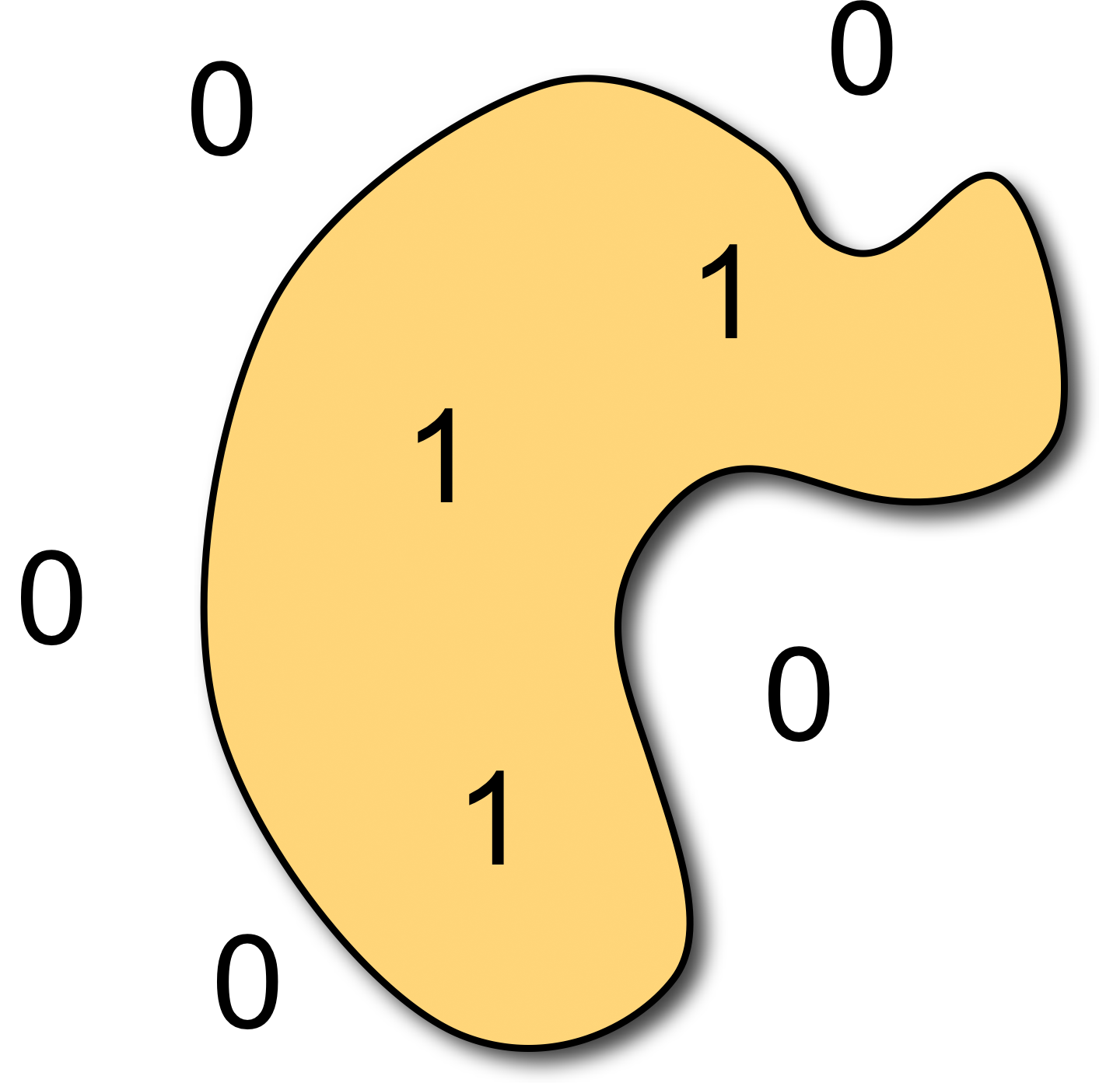
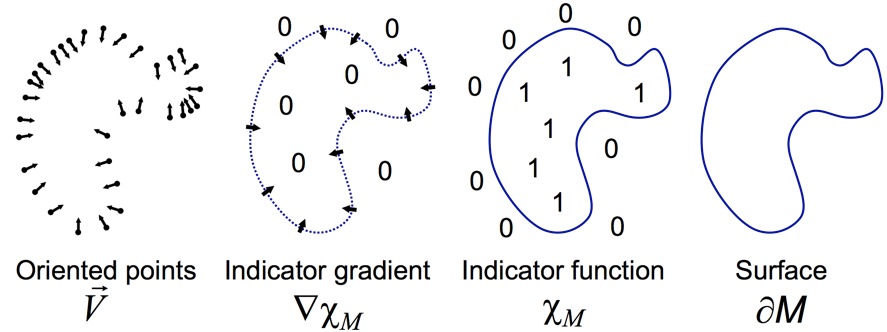
The Indicator Function
- We reconstruct the surface of the model by solving for the indicator function \(\chi\) of the shape
\[\chi(\vec{p}) \;=\; \begin{cases} 1 & \text{if } \vec{p} \in \set{M} \\ 0 & \text{if } \vec{p} \not\in \set{M} \\ \end{cases}\]
Challenge
- How to construct the indicator function from a set of oriented points?


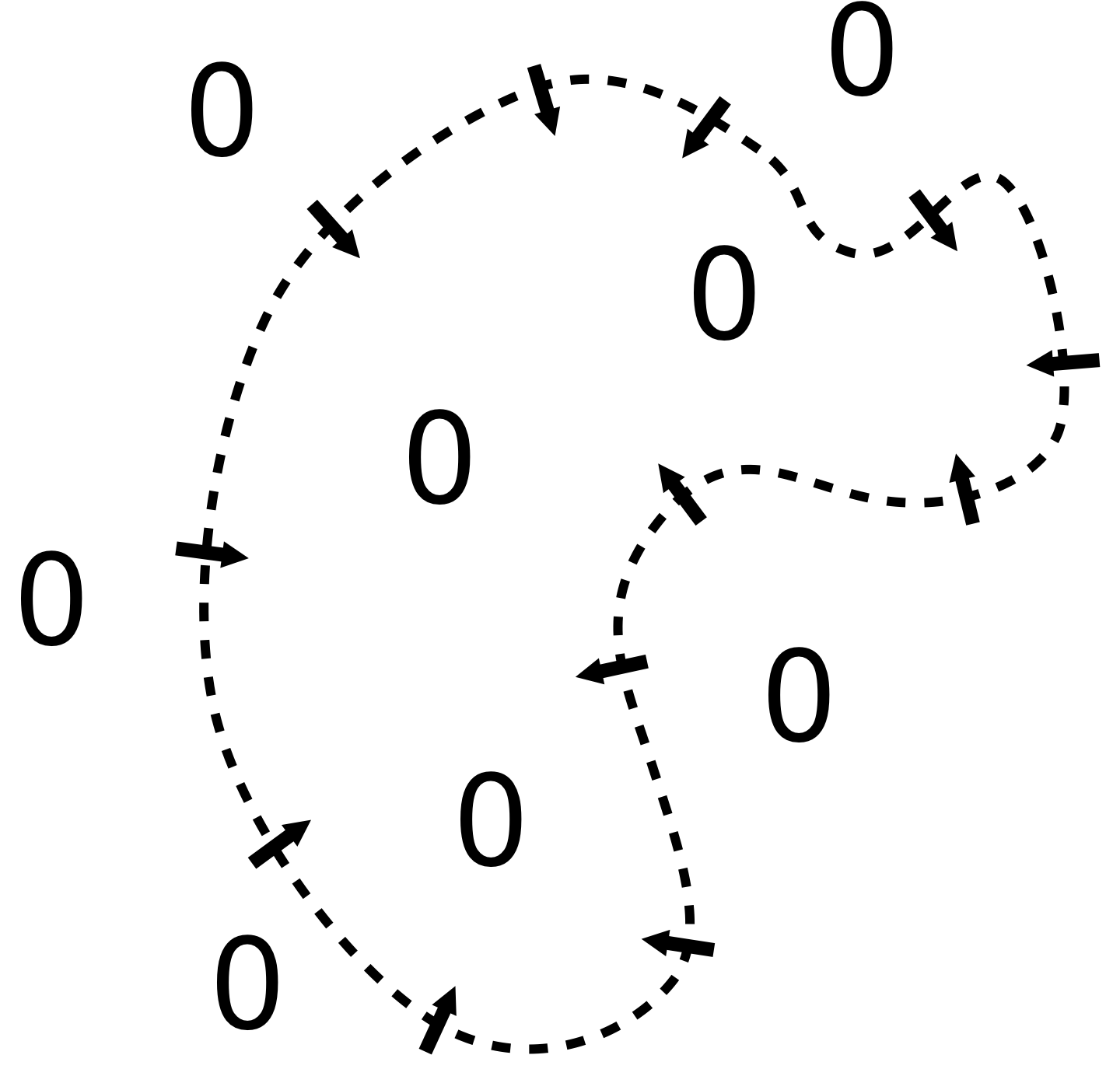
Gradient Relationship
- There is a relationship between the normal field and gradient of (smoothed) indicator function

Recap: Notation
- 3D scalar fields
\[u\of{\vec{x}} \;=\; u(x,y,z)\]
- 3D vector fields
\[\vec{u}\of{\vec{x}} \;=\; \vector{ u(\vec{x}) \\ v(\vec{x}) \\ w(\vec{x}) } \;=\; \vector{ u(x,y,z) \\ v(x,y,z) \\ w(x,y,z) }\]
Recap: Notation
- Gradient & Jacobian
\[\grad u\of{\vec{x}} = \vector{ \diff{u}{x}\of{\vec{x}} \\[1mm] \diff{u}{y}\of{\vec{x}} \\[1mm] \diff{u}{z}\of{\vec{x}} } \,,\quad \grad \vec{u}\of{\vec{x}} = \matrix{ \diff{u}{x}\of{\vec{x}} & \diff{u}{y}\of{\vec{x}} & \diff{u}{z}\of{\vec{x}} \\[1mm] \diff{v}{x}\of{\vec{x}} & \diff{v}{y}\of{\vec{x}} & \diff{v}{z}\of{\vec{x}} \\[1mm] \diff{w}{x}\of{\vec{x}} & \diff{w}{y}\of{\vec{x}} & \diff{w}{z}\of{\vec{x}} }\]
Recap: Notation
- Gradient & Jacobian, simplified notation
- comma-subindex denotes the partial derivative
Recap: Notation
- Divergence
\[\func{div}\of{\vec{u}}\of{\vec{x}} = \left( \grad \cdot \vec{u} \right) \of{\vec{x}} = u_{,x}\of{\vec{x}} + v_{,y}\of{\vec{x}} + w_{,z}\of{\vec{x}}\]
\[\left( \grad \cdot \vec{u} \right) = \vector{ \diff{}{x} \\[1mm] \diff{}{y} \\[1mm] \diff{}{z} } \cdot \vector{ u\of{\vec{x}} \\[1mm] v\of{\vec{x}} \\[1mm] w\of{\vec{x}} } \]
Recap: Notation
- Gradient, Jacobian
\[\grad u\of{\vec{x}} = \vector{ u_{,x}\of{\vec{x}} \\ u_{,y}\of{\vec{x}} \\ u_{,z}\of{\vec{x}} } \,,\quad \grad \vec{u}\of{\vec{x}} = \matrix{ u_{,x}\of{\vec{x}} & u_{,y}\of{\vec{x}} & u_{,z}\of{\vec{x}} \\ v_{,x}\of{\vec{x}} & v_{,y}\of{\vec{x}} & v_{,z}\of{\vec{x}} \\ w_{,x}\of{\vec{x}} & w_{,y}\of{\vec{x}} & w_{,z}\of{\vec{x}} } \]
- Divergence
\[\func{div}\of{\vec{u}}\of{\vec{x}} = \left( \grad \cdot \vec{u} \right) \of{\vec{x}} = u_{,x}\of{\vec{x}} + v_{,y}\of{\vec{x}} + w_{,z}\of{\vec{x}}\]
- Laplace
\[\laplace\vec{u}\of{\vec{x}} \;=\; \grad^2\vec{u}\of{\vec{x}} \;=\; \grad \cdot \grad\vec{u}\of{\vec{x}} \;=\; \vec{u}_{,xx}\of{\vec{x}} + \vec{u}_{,yy}\of{\vec{x}} + \vec{u}_{,zz}\of{\vec{x}}\]
Recap: Notation
- Gradient, Jacobian
\[ \grad u = \vector{ u_{,x} \\ u_{,y} \\ u_{,z} } \,,\quad \grad \vec{u} = \matrix{ u_{,x} & u_{,y} & u_{,z} \\ v_{,x} & v_{,y} & v_{,z} \\ w_{,x} & w_{,y} & w_{,z} } \]
- Divergence
\[\func{div}\of{\vec{u}} = \grad \cdot \vec{u} = u_{,x} + v_{,y} + w_{,z} \]
- Laplace
\[\laplace\vec{u} \;=\; \grad^2\vec{u} \;=\; \grad \cdot \grad\vec{u} \;=\; \vec{u}_{,xx} + \vec{u}_{,yy} + \vec{u}_{,zz} \]
Integration as a Poisson Problem
- Approximate gradients by a vector field \(\vec{v}(\vec{x})\)
- \(\vec{v}(\vec{x}) = \vec{0}\;\) inside and outside
- \(\vec{v}(\vec{p}_i) = \vec{n}_i\;\) at point samples \(\vec{p}_i\) vector field equals point normals \(\vec{n}_i\)
- Find indicator function \(\chi\) whose gradient best approximates \(\vec{v}\) \[\min_{\chi} \int \norm{ \grad\chi (\vec{x}) - \vec{v} (\vec{x})}^2 \func{d}x\]
- not every vector field is integrable, i.e. can be represented as the gradient of a scalar function
- Variational calculus leads to Poisson equation \[\laplace \chi \;=\; \grad \cdot \vec{v}\]
Variational Calculus in 1D
- Minimize deviation from \(v(x)\) on interval \([a,b]\) \[C(f) = \int_a^b \left( f'(x) - v(x) \right)^2 \func{d}x \;\to\;\min\]
- Add test function \(u\) with \(u(a) = u(b) = 0\) \[C\of{f+\lambda u} = \int_a^b \left( f' + \lambda u' - v\right)^2 \func{d}x = \int_a^b \lambda^2 {u'}^2 + 2\lambda (f'-v) u' + \left({f'}-v\right)^2 \func{d}x \]
- If f minimizes C, the following has to vanish \[ \left. \frac{\partial C\of{f+\lambda u}}{\partial \lambda} \right|_{\lambda=0} \;=\; \int_a^b 2 (f'-v) u' \, \func{d}x \;\stackrel{!}{=}\; 0 \]
Variational Calculus in 1D
- Has to vanish for any \(u\) with \(u(a) = u(b) = 0\) \[ \int_a^b (f'-v)u' \, \func{d}x \;=\; \underbrace{\left[ (f'-v) u \right]_a^b}_{=0} - \int_a^b (f''-v')u \, \func{d}x \;\stackrel{!}{=}\; 0 \quad \forall u \]
- Only possible if \[ f'' - v' \;=\; 0 \quad\Leftrightarrow\quad \laplace f = \grad \cdot v \]
- So-called Euler-Lagrange Equation
Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
- Compute indicator function
- Extract iso-surface

Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
- Compute indicator function
- Extract iso-surface

Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
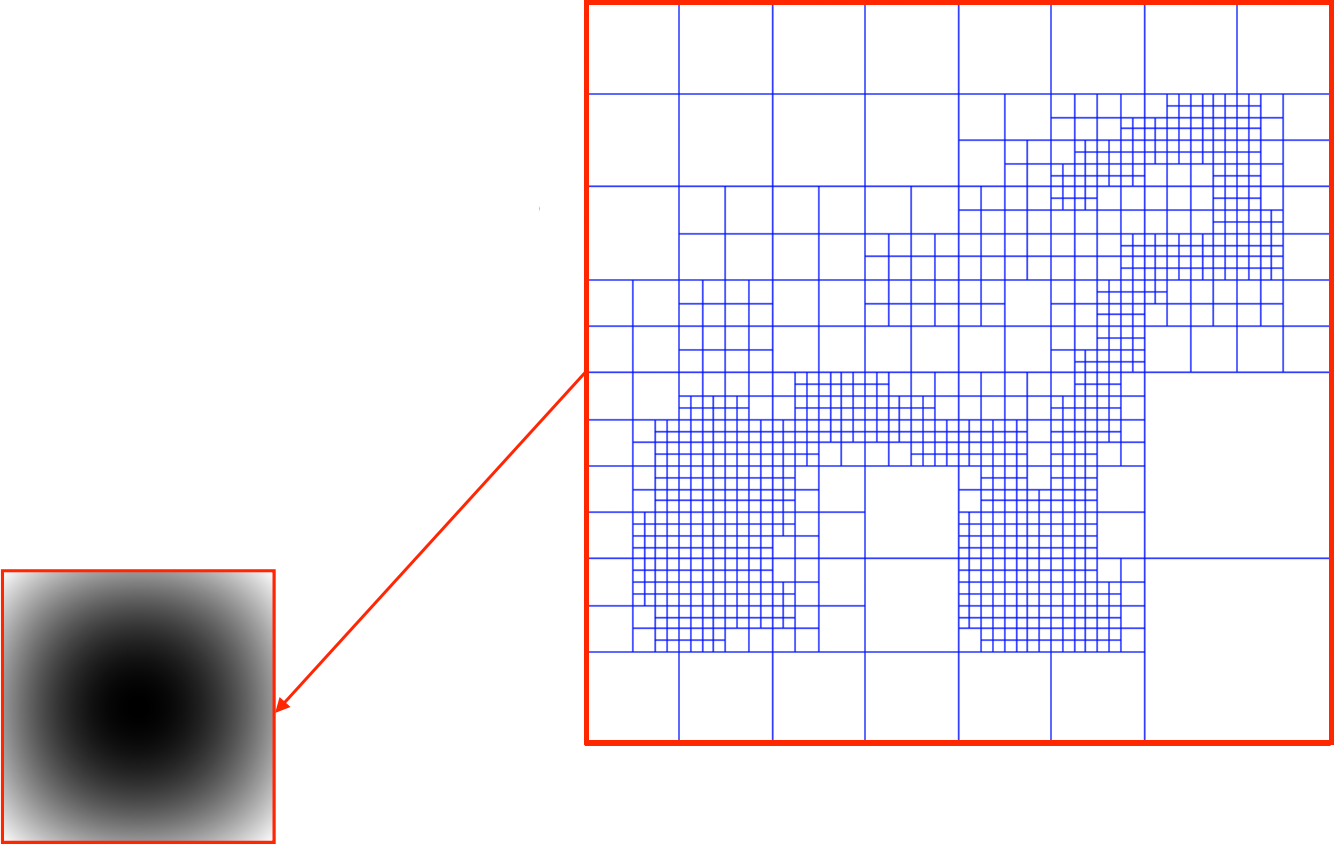
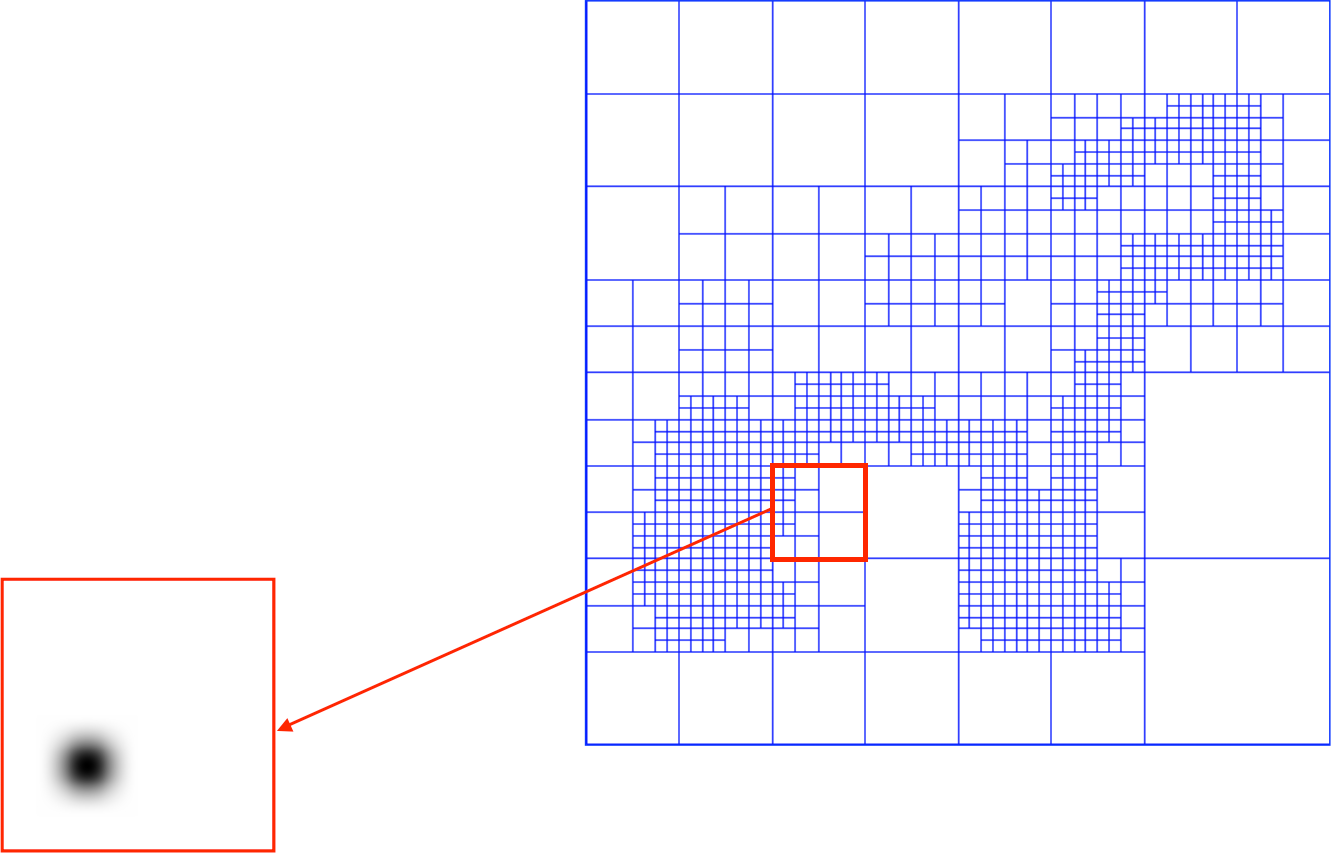
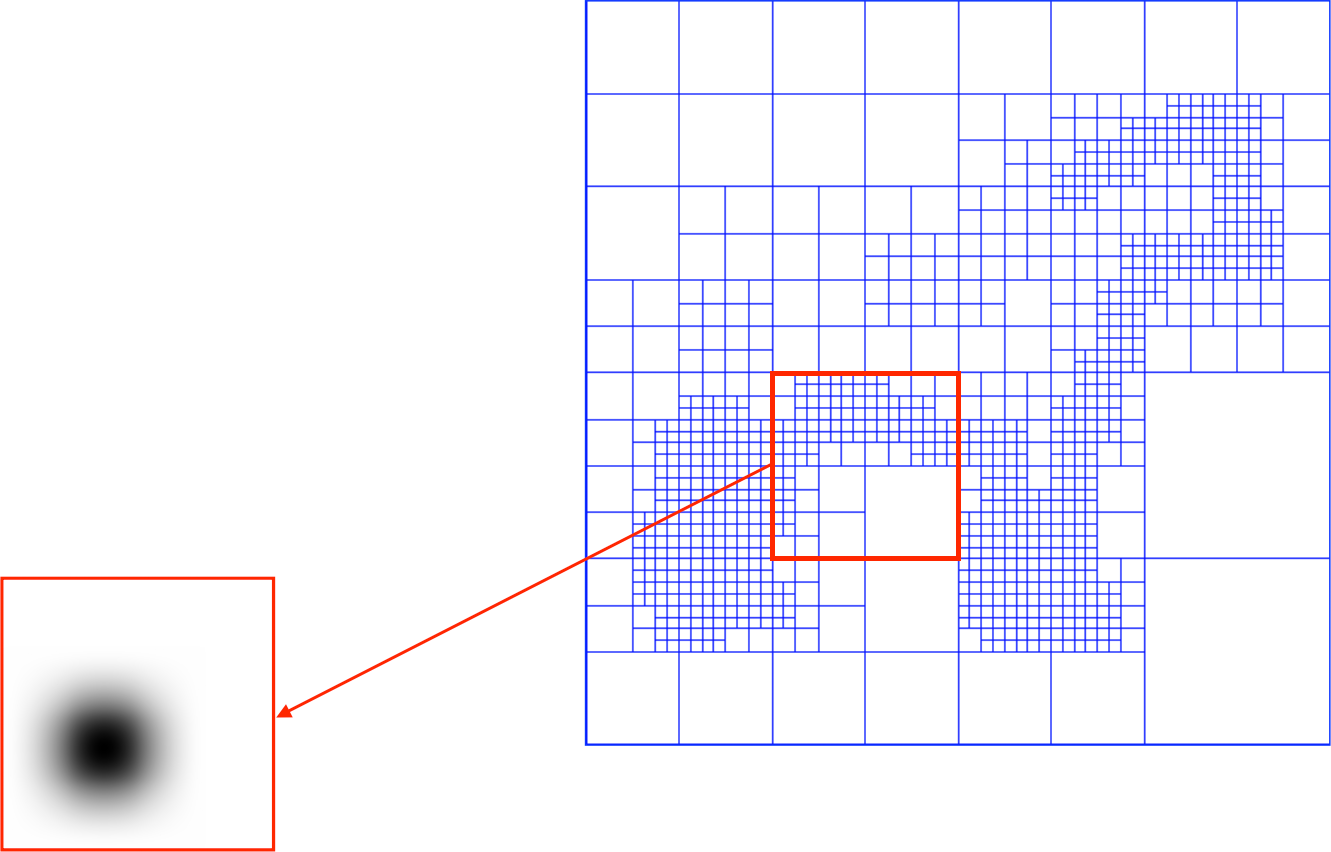
- Define function basis
- Splat the samples
- Compute indicator function
- Extract iso-surface
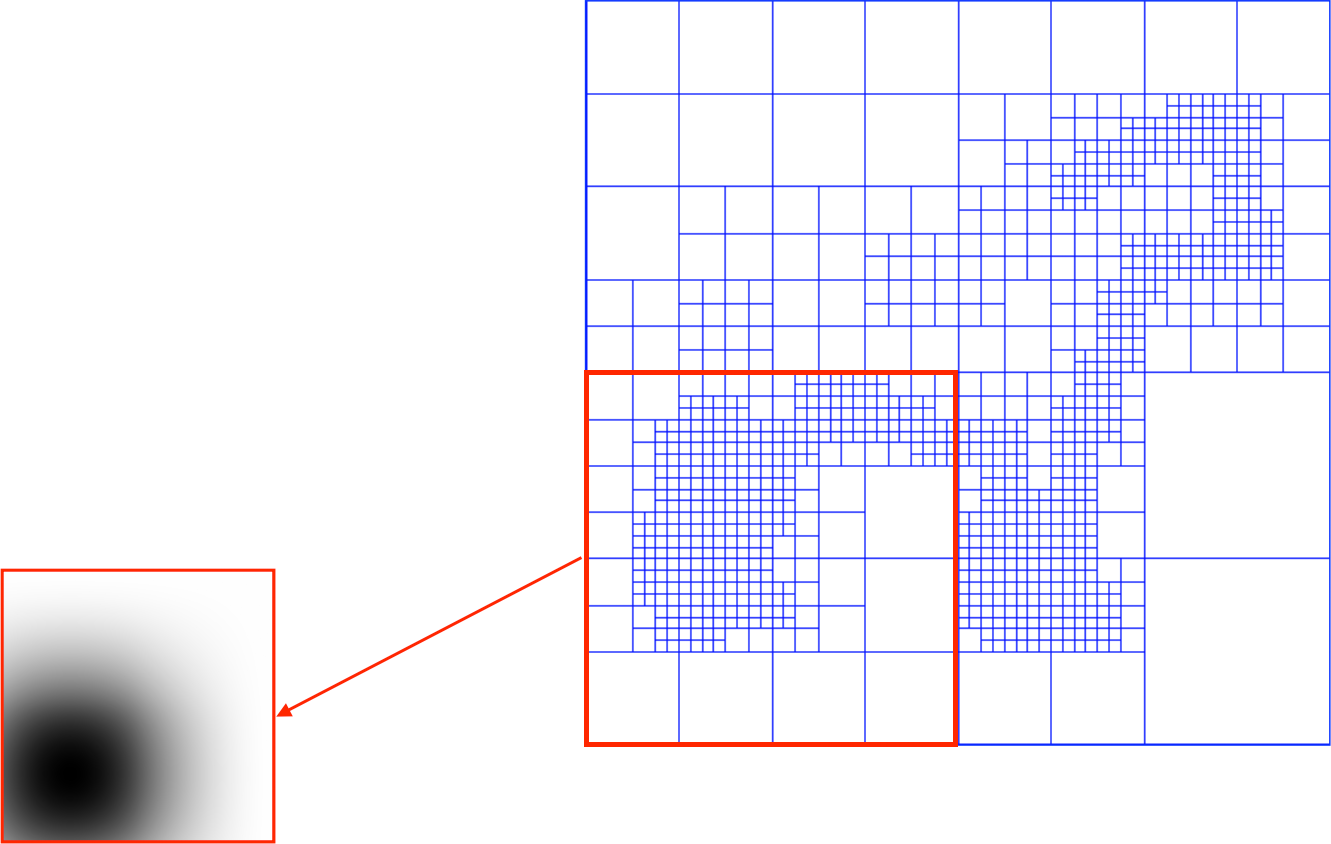
Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
- Define function basis
- Splat the samples
- Compute indicator function
- Extract iso-surface
Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
- Define function basis
- Splat the samples
- Compute indicator function
- Extract iso-surface
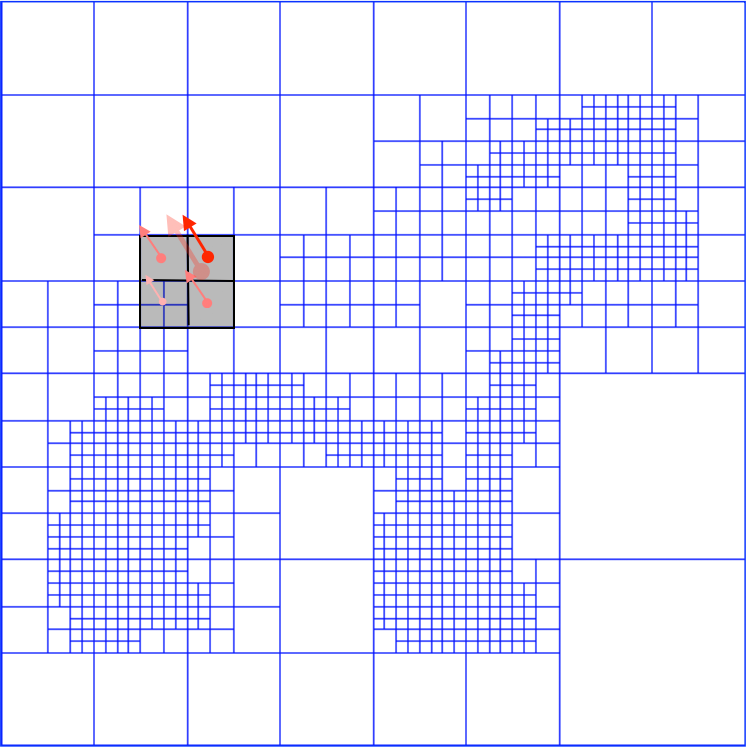
Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
- Define function basis
- Splat the samples
- Compute indicator function
- Extract iso-surface

Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
- Compute indicator function
- Compute divergence
- Solve Poisson equation
- Extract iso-surface

Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
- Compute indicator function
- Compute divergence
- Solve Poisson equation
- Extract iso-surface




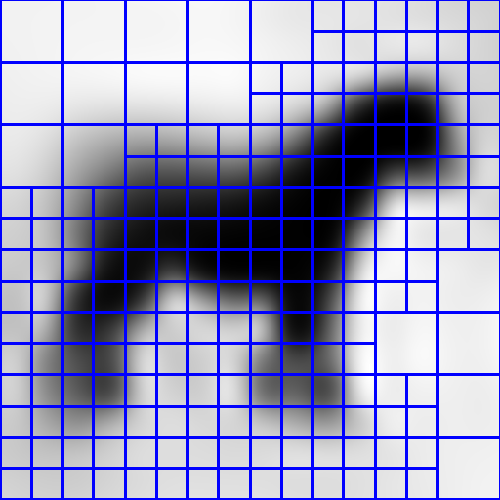

Implementation
- Given the input point set:
- Setup adaptive octree
- Compute vector field
- Compute indicator function
- Extract iso-surface

Poisson Surface Reconstruction
- Summary
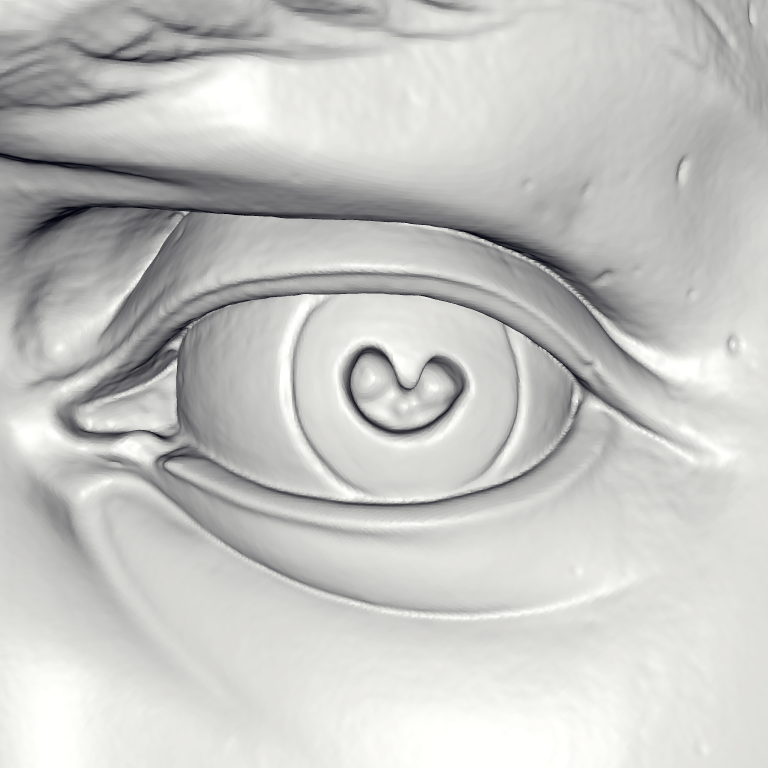
Michelangelo’s David
- 215 million data points from 1000 scans
- 22 million triangle reconstruction
- Compute time: 2.1 hours
- Peak memory: 6600MB


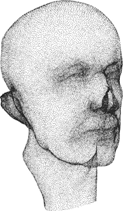
Face Scans
- Performs de-noising and smooth hole filling
- Adaptive octree yields detailed reconstruction



Summary
- Poisson Surface Reconstruction
- robustness to outliers
- fills holes
- performance through octree and multilevel solver
- can also be implemented on tetrahedral mesh (CGAL implementation )