Last time - Implicit Representation
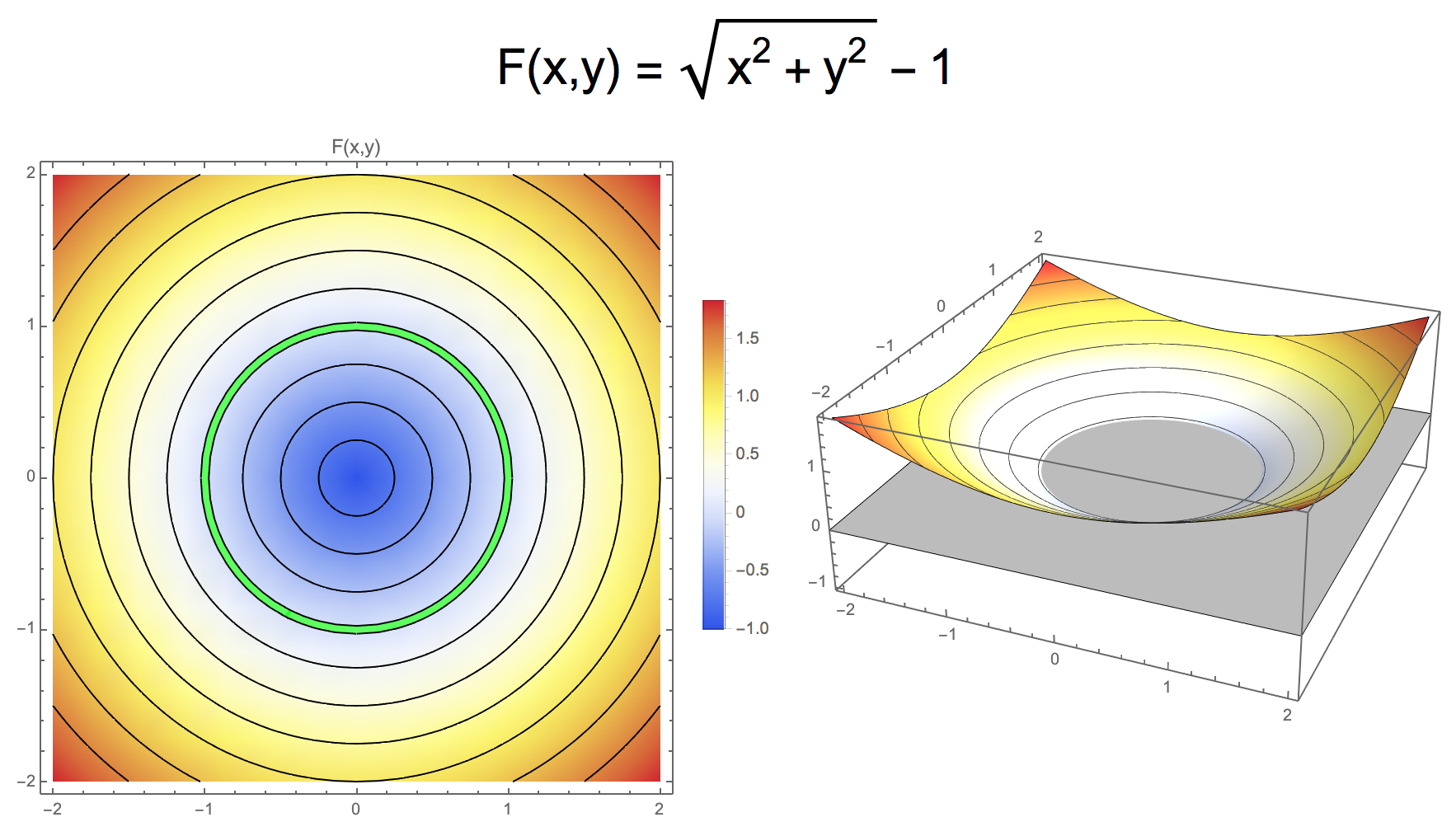
- Implicit function defines a closed surface at \(F(\vec{x}) = 0\) embedded in \(\R^n\) that separates space into inside and outside
- Typical convention for sign
- Interior: \(F(\vec{x}) < 0\)
- Exterior: \(F(\vec{x}) > 0\)
Last time - 2D Marching Squares
Last time - Implicit Representations
- Summary
- Kernel of function \(F \colon \R^n \to \R\), i.e. \(\{\vec{x} \in \R^n \mid F(\vec{x}) = 0\}\) defines closed surface, gradient \(\nabla F\) defines surface normal
- Signed Distance Function (SDF) as special case with unique properties
- Modeling with functions is hard → discrete representation
- Marching squares (cubes) to reconstruct level set from grid
- Pros
- Easy to determine if point is inside or outside (e.g. for collision detection)
- Easy to handle topology changes
- Cons
- Hard to generate points on surface (e.g. for rendering) or to modify geometry (e.g. deform surface)
Last time - Parametric Representation
- Parametric representation \(\vec{x}: [a,b] \subset \R \mapsto \R^2\)
\[\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t}}\]
- Curve is defined as image of interval \([a,b]\) under parameterization function \(\vec{x}\).
- Re-parametrization \(\vec{x}(u) = \vec{x}\of{t(u)}\)
- Curve arc length \[ L = \int_a^b \norm{\vec{x}’} \mathrm{d}t = \int_a^b \sqrt{\left(\frac{\mathrm{d} x}{\mathrm{d} t} \right)^2 + \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t \]
Overview for Today
Differential Geometry of parametric curves
- Tangent vector, normal vector
- Arc length parameterization
- Curvature, osculating circle, discrete curvature
- A first application: Curve smoothing
Differential Geometry of parametric surfaces
- tangent space, metric, first fundamental form
- normal curvature
- principal curvatures
- Mean & Gaussian curvature
- Minimal and developable surfaces
Tangent & Normal
Parametric representation of planar curve \(\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t}}\)
First derivative defines a tangent vector
\[\vec{t} = \vec{x}’\of{t} := \frac{\mathrm{d} \vec{x}\of{t}}{\mathrm{d} t} = \matrix{ \mathrm{d}x\of{t} / \mathrm{d} t \\ \mathrm{d}y\of{t} / \mathrm{d} t}\]
The curve normal vector is
\[\vec{n} = \text{Rot}(90) \frac{\vec{t}}{\| \vec{t} \|}\]
Tangent & Normal
- Example: \(\vec{x}\of{t} = (1+\cos(t)) \matrix{\cos(t) \\ \sin(t)}\)
Curve as Particle Trajectory
- Curve parameter \(t\) is time
- \(\vec{x}\of{t}\) defines the position of particle at time \(t\)
- Tangent \(\vec{x}’\of{t}\) defines the velocity vector at time \(t\)
- Length (magnitude) of tangent vector is particle speed
Curve as Particle Trajectory
- Recall: Re-parameterization
- Example
- For \(t \in [0, 1]\), the two curves \(\vec{x}_1(t) = \matrix{\cos\of{ t} \\ \sin\of{ t}}\) and \(\vec{x}_2(t) = \matrix{\cos\of{ t^2} \\ \sin\of{ t^2}}\) define the same particle path
- However, particles travel with different speed!
- \(\norm{\vec{x}’_1(t)} = 1\)
- \(\norm{\vec{x}’_2(t)} = \sqrt{ (-2t \sin\of{ t^2})^2 + (2t \cos\of{ t^2})^2 } = 2|t|\)
Arc Length Parameterization
- We see that a curve can be parameterized in different ways. But is there a unique, canonical way to parameterize a curve?
- Yes! It’s called arc length parameterization
- Parameterize curve \(\vec{x}(s)\) over interval \([0, L]\) such that length from \(\vec{x}(0)\) to \(\vec{x}(s)\) is equal to \(s\) \[\int_0^s \norm{\vec{x}'(t)}\func{d}t \;=\; s\]
Arc Length Parameterization
- Intuitively, think about a rope of length \(L = \int \norm{\vec{x}’} \mathrm{d}t\) that is bend (but not stretched or compressed!) to assume the shape of the curve

- Curves parameterized with respect to arc length have some useful properties
- Unit speed: \(\norm{ \vec{x}'(s) } = 1\)
- Orthogonality: \(\vec{x}'(s) \cdot \vec{x}''(s) = 0\)
Curvature
- Curvature is a measure of how much the curve deviates from a straight line
- This can be quantified by looking at how much the curve normal varies as we traverse the curve
- The curve normal vector is \(\vec{n} = \text{Rot}(90) \frac{\vec{t}}{\| \vec{t} \|}\)
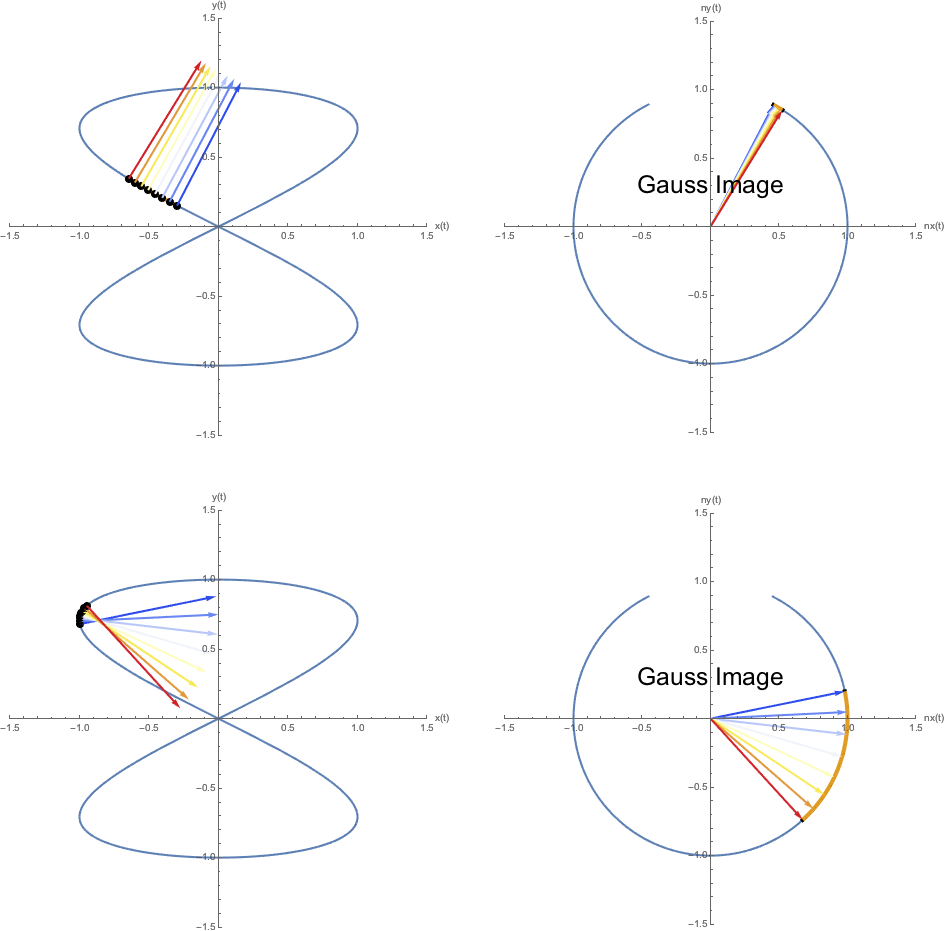
- The Gauss map of the curve \(\vec{x}\of{t}\) maps the parameter interval \([a,b]\) to the unit circle: \(\vec{n}: [a,b] \mapsto S^1\)
- This means that for every \(t \in [a,b]\) we obtain a point on the unit circle defined by the curve normal \(\vec{n}(t)\) at point \(\vec{x}\of{t}\)
Gauss Map
Curvature
- Let \(\Omega = [t-\epsilon, t+\epsilon]\) be a small interval around parameter \(t\), \(l_{\vec{x}}\of{\epsilon}\) be the length of the curve segment \(\vec{x}\of{\Omega}\), and \(l_{\vec{n}}\of{\epsilon}\) be the length of the corresponding segment of the Gauss map
- Then the magnitude of the curvature at point \(\vec{x}\of{t}\) is def. as \[|\kappa \of{t}| = \lim_{\epsilon \rightarrow 0} \frac{l_{\vec{n}}\of{\epsilon}}{l_{\vec{x}}\of{\epsilon}}\]
- If a curve is parameterized by arc length, then curvature is simply the magnitude of the second derivative \[ \vec{t}'(s) = \vec{x}''(s) = \kappa\of{s} \vec{n}(s) \; \rightarrow \; |\kappa\of{s}| = | \vec{x}''(s) | \]
- For general parametrizations \(\quad \kappa \of{t} = \frac{ || \vec{x}'(t) \times \vec{x}''(t) || }{ ||\vec{x}'(t)||^3 }\)
Curvature
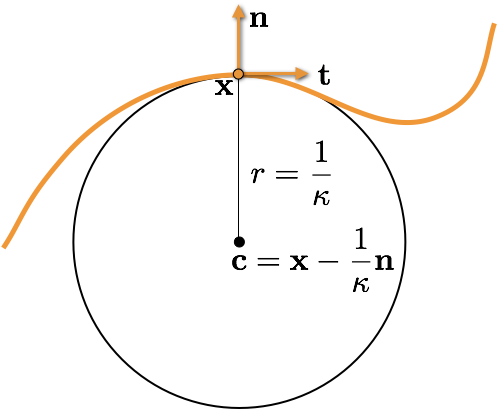
- The osculating circle at point \(\vec{x}\) is the circle tangent to the curve at \(\vec{x}\) that best approximates the curve locally
- Its center is given as \(\vec{x} + \frac{1}{\kappa} \vec{n}\), where \(\kappa\) is the signed curvature and \(\vec{n}\) is the normal at \(\vec{x}\).
- Its radius is the inverse of the absolute curvature, i.e. \(1/|\kappa|\)
Curvature
Discrete Curvature
- How can we define curvature on a polyline?
- Continuous definition does not makes sense. Curvature would be zero on line segment and infinite at vertices. Polyline is not differentiable!
- Consider polyline as approximation of a smooth curve
- Approximate osculating circle by circle passing through three adjacent points
- Aside: Prove that any three distinct points define a unique circle!
Discrete Curvature
Which of the following is true?
A First Application
- Discrete Curve Smoothing
- Variant A: Curvature Flow
- For each vertex, compute the discrete osculating circle
- Move every vertex towards the center of circle
- Iterate!
- Variant B: Laplacian Smoothing
- For each vertex, compute the average of its two neighbors
- Move every vertex towards the average
- Iterate!
Discrete Laplacian Curve Smoothing
number of iterations per frame increases towards end of video
Discrete Curve Smoothing
- Stay tuned, we will study this in a lot more detail!
- In particular, we will see how to properly discretize the underlying PDEs
In the meantime, think about the following questions:
- Does any closed polyline converge under this flow?
- If so, to what?
- What else can you say about how the shape evolves?
Experiment with your implementation to gain insight into these questions
Overview
- Differential Geometry of parametric curves
- Differential Geometry of parametric surfaces
- tangent space, metric, first fundamental form
- normal curvature
- principal curvatures
- Mean & Gaussian curvature
- Minimal and developable surfaces
Parametric Surfaces
- Continuous surface \[\vec{x}\of{u,v} = \matrix{ x\of{u,v} \\ y\of{u,v} \\ z\of{u,v} }\]
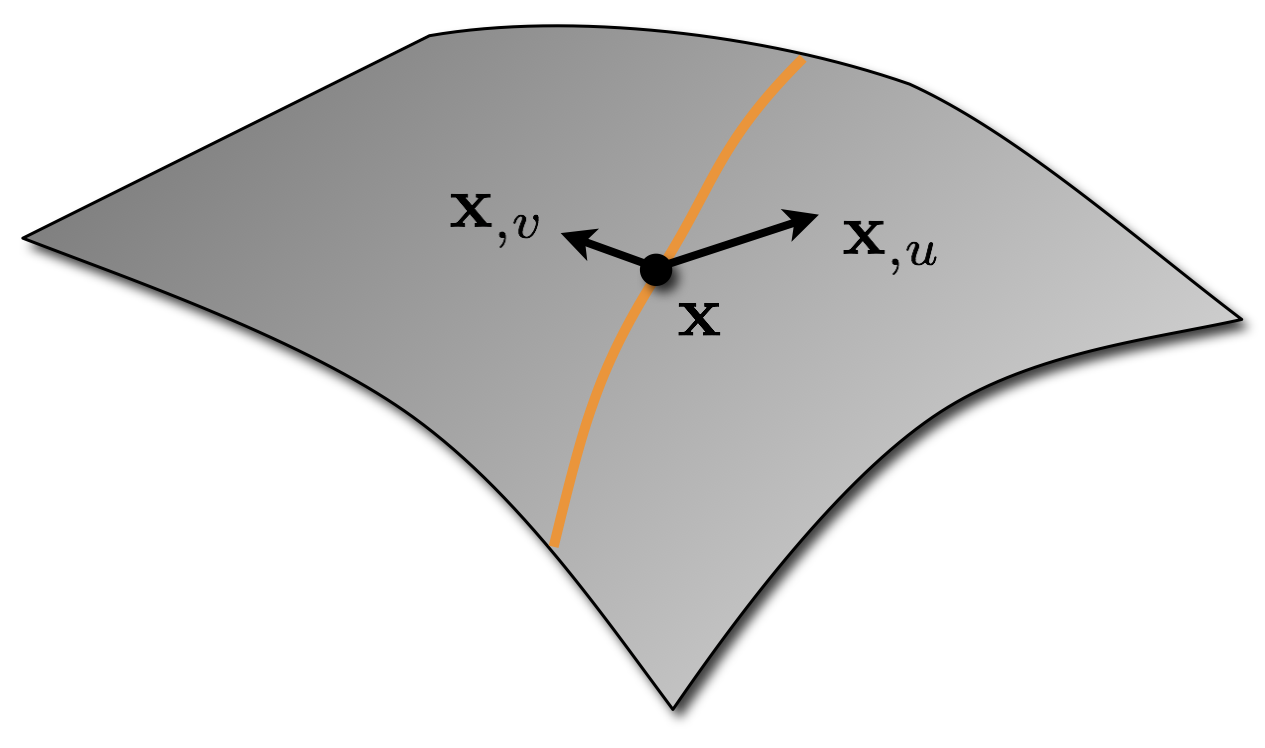
Curves on Surface
- A curve \((u(t), v(t))\) in the \(uv\)-plane defines a curve on the surface \(\vec{x}(u,v)\): \[\vec{x}\of{t} \;=\; \vec{x}\of{ u\of{t}, v\of{t} }\]
Tangent Vectors of Curves on Surface
- Curve on surface \(\vec{x}\of{t} \;=\; \vec{x}\of{ u\of{t}, v\of{t} }\)
- Tangent vector to curve \[\begin{eqnarray} \vec{x}\of{t}' & = & \frac{d \vec{x}\of{t}}{dt} \end{eqnarray}\]
Tangent Vectors of Curves on Surface
- Curve on surface \(\vec{x}\of{t} \;=\; \vec{x}\of{ u\of{t}, v\of{t} }\)
- Tangent vector to curve \[\begin{eqnarray} \vec{x}\of{t}' & = & \frac{d \vec{x}\of{t}}{dt} = \frac{d}{dt}\left( \vec{x}\of{u(t), v(t)} \right) \\ & = & \frac{\partial \vec{x}}{\partial u} \cdot \frac{du}{dt} + \frac{\partial \vec{x}}{\partial v} \cdot \frac{dv}{dt} \\ & = & \left[ \vec{x}_{,u}, \vec{x}_{,v}\right] \left[ \begin{array}{c} u' \\ v' \end{array}\right]\\ & = & J \vec{u}' \end{eqnarray}\]
- Jacobian matrix \(J \in \mathbb{R}^{3\times 2}\) defines mapping of tangent vectors from the domain to the surface: \(\vec{u}' \mapsto \vec{x}'\)
- Tangent plane is formed by linear combinations of \(\vec{x}_{,u}\) and \(\vec{x}_{,v}\)
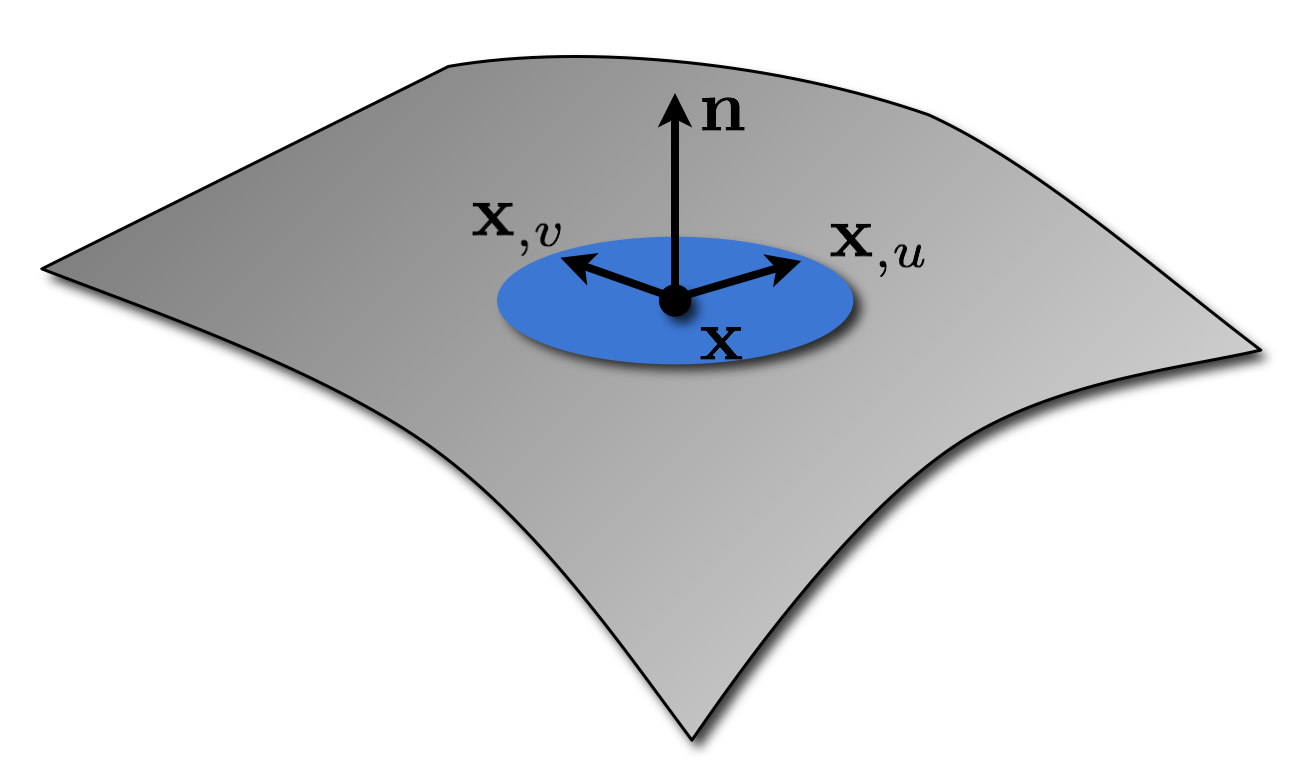
Parametric Surfaces
- Continuous surface \[\vec{x}\of{u,v} = \matrix{ x\of{u,v} \\ y\of{u,v} \\ z\of{u,v} }\]
- Normal vector \[\vec{n} = \frac{\vec{x}_{,u} \times \vec{x}_{,v}}{\norm{\vec{x}_{,u} \times \vec{x}_{,v}}}\]
- Assume regular parameterization \[\vec{x}_{,u} \times \vec{x}_{,v} \neq \vec{0}\]
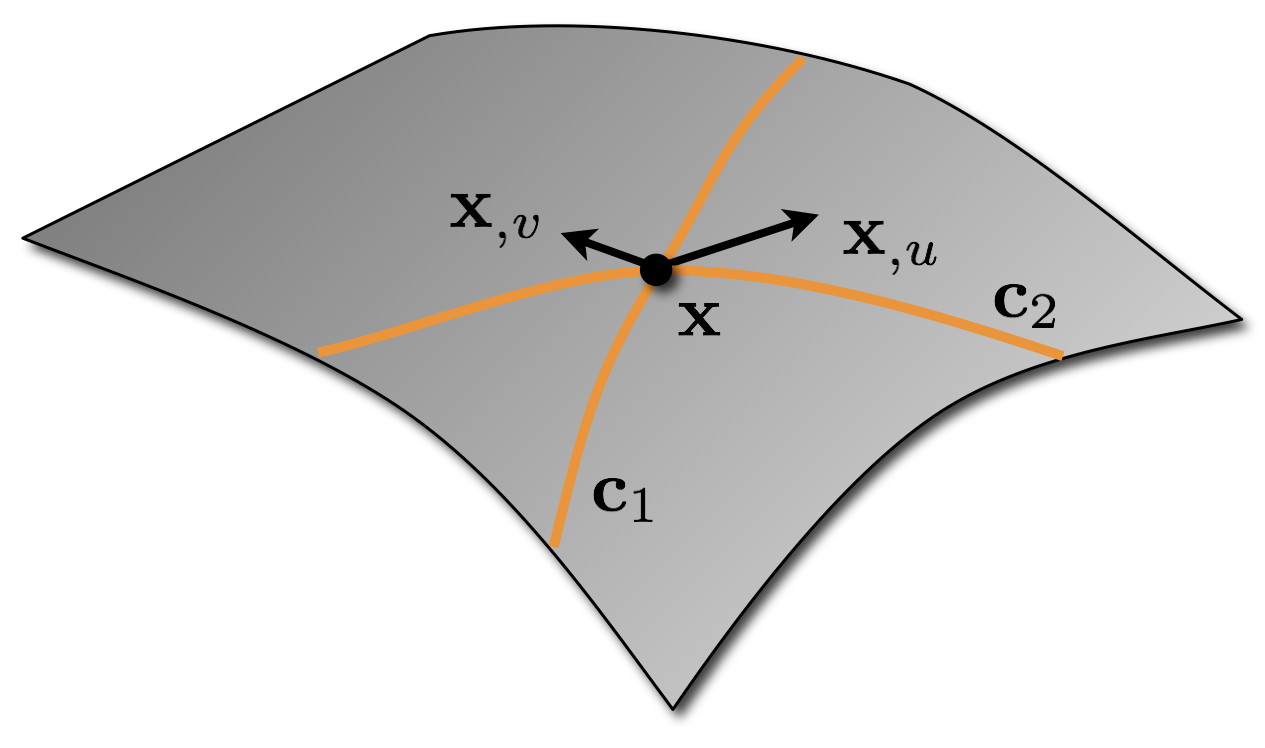
Angles on Surface
- What is the angle of intersection of two curves \(\vec{c}_1\) and \(\vec{c}_2\) intersecting at \(\vec{x}\)?
- Two tangents \(\vec{t}_1\) and \(\vec{t}_2\) \[ \vec{t}_i = \alpha_i \vec{x}_{,u} + \beta_i \vec{x}_{,v} \]
- Compute inner product \[ \begin{align} \trans{\vec{t}_1} \vec{t}_2 \;&=\; \cos\theta \norm{\vec{t}_1} \norm{\vec{t}_2} \\ \;&=\; \trans{\left(\alpha_1 \vec{x}_{,u} + \beta_1 \vec{x}_{,v} \right)} \left(\alpha_2 \vec{x}_{,u} + \beta_2 \vec{x}_{,v} \right) \\ \;&=\; \left( \alpha_1, \beta_1 \right) \matrix{ \trans{\vec{x}_{,u}} \vec{x}_{,u} & \trans{\vec{x}_{,u}} \vec{x}_{,v} \\[1mm] \trans{\vec{x}_{,u}} \vec{x}_{,v} & \trans{\vec{x}_{,v}} \vec{x}_{,v} } \matrix{\alpha_2 \\ \beta_2 } \end{align} \]
First Fundamental Form
- First fundamental form
\[\mat{I} \;=\; \matrix{ E & F \\ F & G } \;:=\; \matrix{ \vec{x}_{,u}^T\vec{x}_{,u} & \vec{x}_{,u}^T\vec{x}_{,v} \\[1mm] \vec{x}_{,u}^T\vec{x}_{,v} & \vec{x}_{,v}^T\vec{x}_{,v} }\]
- Defines inner product on tangent space
\[\begin{eqnarray*} \left\langle \matrix{\alpha_1 \\ \beta_1} \,,\; \matrix{\alpha_2 \\ \beta_2} \right\rangle \;:=\; \matrix{\alpha_1 \\ \beta_1}^T \mat{I} \, \matrix{\alpha_2 \\ \beta_2} \end{eqnarray*} \]
First Fundamental Form
Wikipedia: First Fundamental Form
First fundamental form allows to measure…
- Angles
\(\begin{align} \vec{t}_1^T\vec{t}_2 \;&=\; \left\langle (\alpha_1, \beta_1), (\alpha_2, \beta_2) \right\rangle \\ \;&=\; E \alpha_1\alpha_2 + F\left( \alpha_1\beta_2 + \alpha_2\beta_1 \right) + G \beta_1\beta_2 \end{align}\)
- Length
\(\begin{align} \func{d}s \;&=\; \sqrt{\left\langle (\func{d}u, \func{d}v), (\func{d}u, \func{d}v) \right\rangle} \\ \;&=\; \sqrt{E\,\func{d}u^2 + 2F\,\func{d}u\func{d}v + G\,\func{d}v^2} \end{align}\)
- Area
\(\begin{align} \func{d}A \;&=\; \sqrt{\func{det}\of{\mat{I}}} \,\func{d}u\,\func{d}v \\ \;&=\; \sqrt{EG-F^2} \,\func{d}u\,\func{d}v \end{align}\)
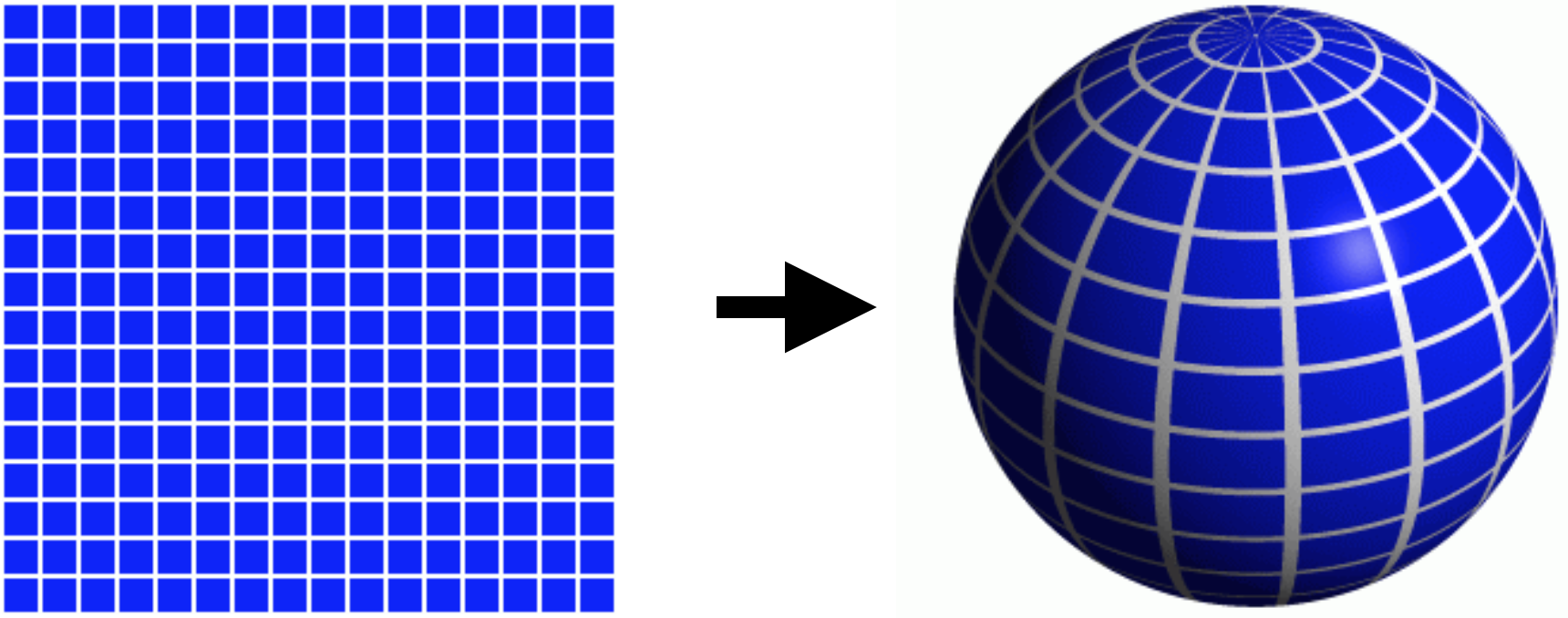
Example: Unit Sphere
- Spherical parameterization
\[\vec{x}\of{u,v} \;=\; \matrix{\cos u \sin v \\ \sin u \sin v \\ \cos v} \,,\quad (u,v) \in [0, 2\pi) \times [0,\pi) \]
Example: Unit Sphere
- Tangent vectors \[ \vec{x}_{,u}\of{u,v} \;=\; \matrix{-\sin u \sin v \\ \cos u \sin v \\ 0} \quad \vec{x}_{,v}\of{u,v} \;=\; \matrix{\cos u \cos v \\ \sin u \cos v \\-\sin v} \]
- First fundamental form \[ \mat{I} \;=\; \matrix{ E & F \\ F & G } \;:=\; \matrix{ \trans{\vec{x}_{,u}} \vec{x}_{,u} & \trans{\vec{x}_{,u}} \vec{x}_{,v} \\[1mm] \trans{\vec{x}_{,u}} \vec{x}_{,v} & \trans{\vec{x}_{,v}} \vec{x}_{,v} } \; = \; \matrix{ \sin^2 v & 0 \\ 0 & 1 } \]
Example: Unit Sphere
- Length of equator \(\vec{x}(t, \pi / 2)\)
- \(u(t)=t\) and \(u'(t)=1\)
- \(v(t)=\pi/2\) and \(v'(t)=0\)

\[ \begin{align} \int_0^{2\pi} 1 \,\func{d}s \;&=\; \int_0^{2\pi} \sqrt{E \, u_{,t}^2 + 2F \, u_{,t} v_{,t} + G \, v_{,t}^2} \,\func{d}t \\ \;&=\; \int_0^{2\pi} \sin v \,\func{d}t \\ \;&=\; 2\pi \sin v \;=\; 2\pi \end{align} \]
Example: Unit Sphere
- Area of sphere

\[ \begin{align} \int_0^{\pi}\int_0^{2\pi} 1 \,\func{d}A \;&=\; \int_0^{\pi}\int_0^{2\pi} \sqrt{EG-F^2} \,\func{d}u\,\func{d}v \\ \;&=\; \int_0^{\pi}\int_0^{2\pi} \sin v \,\func{d}u\,\func{d}v \\ \;&=\; 4\pi \end{align} \]
Normal Curvature
- Let \(\vec{t}\) be a tangent vector at \(\vec{x}\).
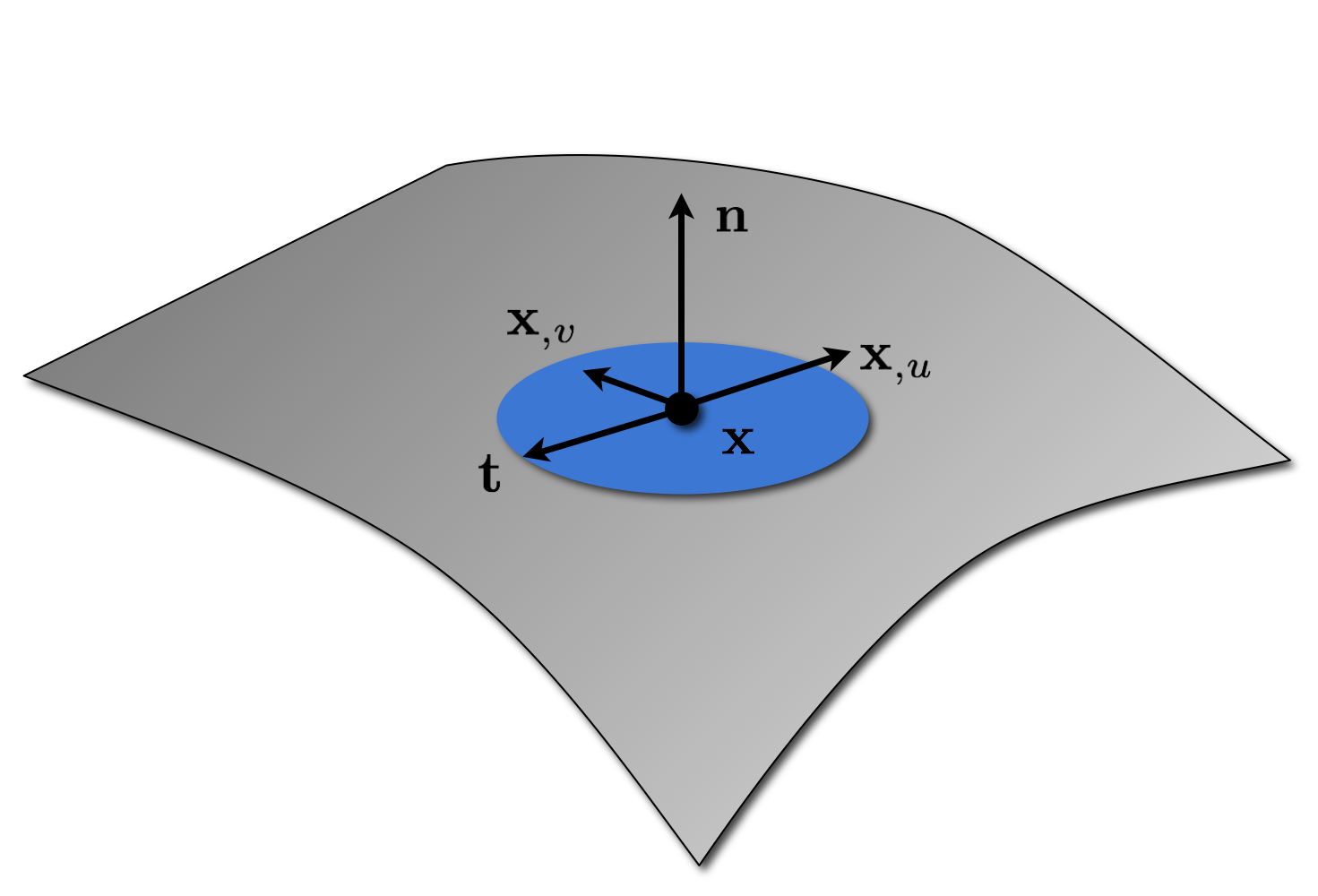
Normal Curvature
- Let \(\vec{t}\) be a tangent vector at \(\vec{x}\).
- \(\vec{x}\), \(\vec{n}\), and \(\vec{t}\) define a normal plane. The intersection of this plane with the surface yields a curve \(\vec{x}(t)\), called a normal section.
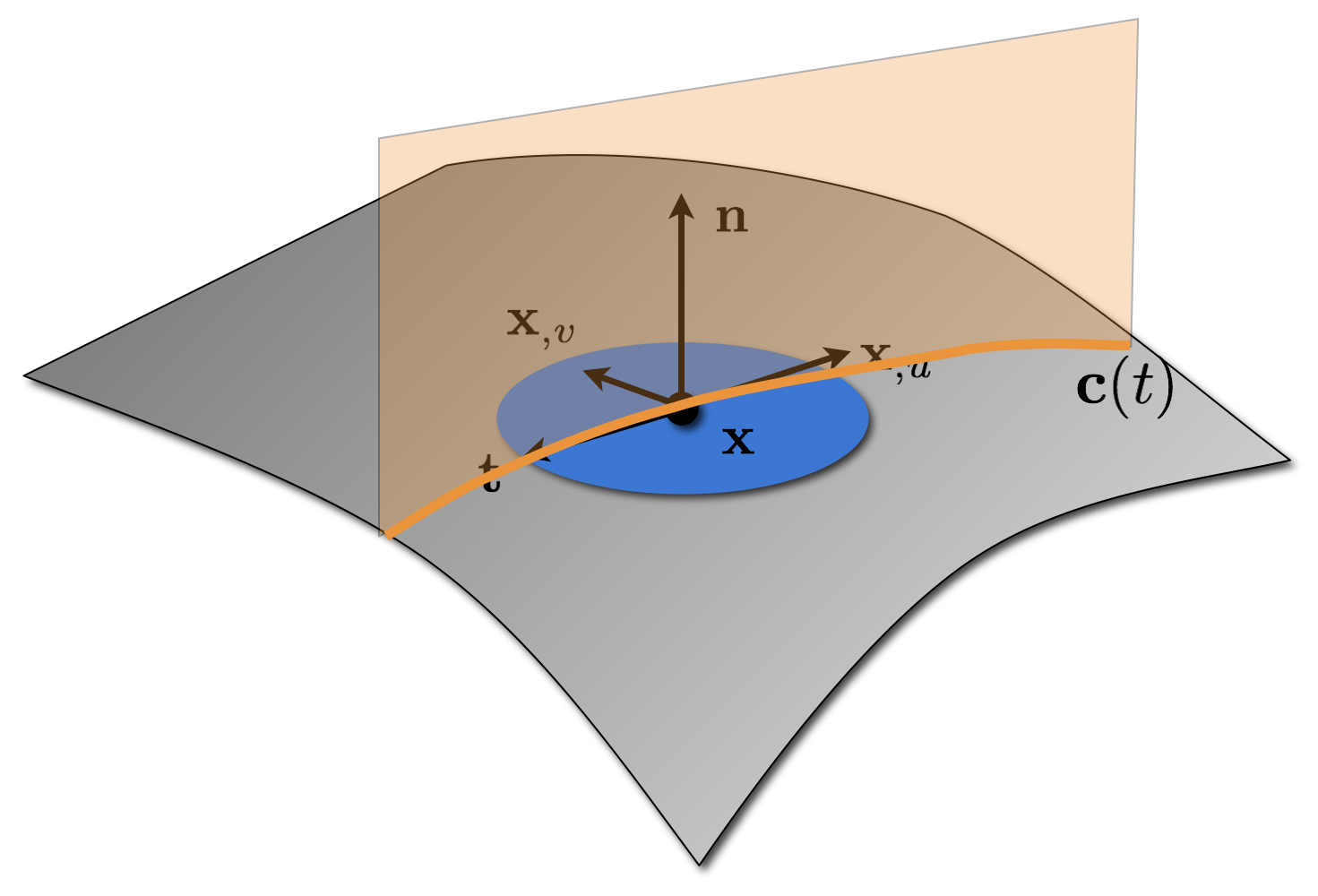
Normal Curvature
- Normal curvature \(\kappa_n(\vec{t})\) is defined as the curvature of the normal section \(\vec{x}(t)\) at the point \(\vec{x}(u,v)\).
- If we write \(\vec{t} = a\vec{x}_{,u} + b\vec{x}_{,v}\), the normal curvature can be computed as
\[ \kappa_n\of{\vec{t}} \;=\; \frac{ (a,b) \, \mat{I\!I} \, \trans{(a,b)} }{ (a,b) \, \mat{I} \, \trans{(a,b)} } \;=\; \frac{ea^2+2fab+gb^2}{Ea^2+2Fab+Gb^2}\]with the second fundamental form\[\mat{I\!I} \;=\; \matrix{e & f \\ f & g} \;:=\; \matrix{ \trans{\vec{x}_{,uu}} \vec{n} & \trans{\vec{x}_{,uv}} \vec{n} \\[1mm] \trans{\vec{x}_{,uv}} \vec{n} & \trans{\vec{x}_{,vv}} \vec{n} }\]
Normal Curvature
- Let \(\vec{t}(\phi) = \cos \phi \vec{x}_{,u} + \sin \phi \vec{x}_{,v}\) be a tangent vector at \(\vec{x}\) and assume that \(\vec{x}_{,u}\) and \(\vec{x}_{,v}\) are orthonormal.
- We can plot \(\kappa_n(\vec{t}(\phi))\) as a function of the tangent angle \(\phi\)
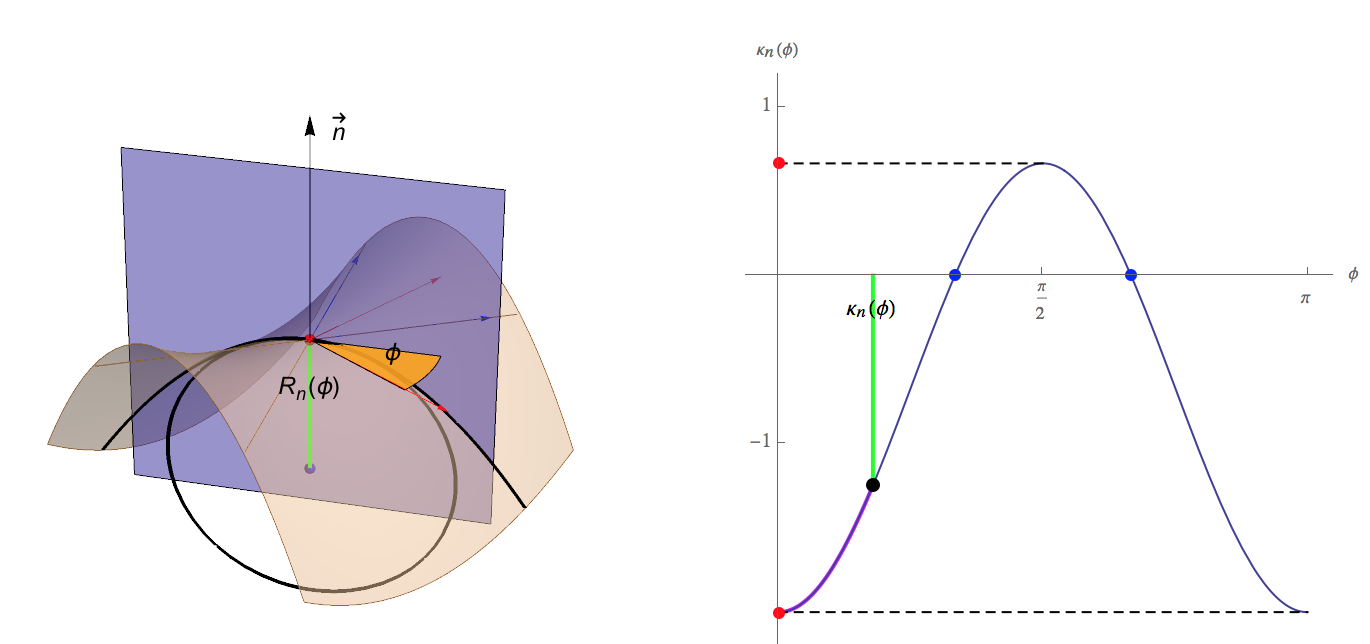
Surface Curvature(s)
- Principal curvatures
- Maximum curvature \(\kappa_1 = \max_{\phi} \kappa_n(\phi)\)
- Minimum curvature \(\kappa_2 = \min_{\phi} \kappa_n(\phi)\)
- Euler theorem: \(\kappa_n\of{\phi} \;=\; \kappa_1\cos^2\phi + \kappa_2\sin^2\phi\)
- Corresponding principal directions \(\vec{e}_1\), \(\vec{e}_2\) are orthogonal
- Maximum curvature \(\kappa_1 = \max_{\phi} \kappa_n(\phi)\)
Surface Curvature(s)
- Special curvatures
- Mean curvature \(H= \frac{1}{2\pi} \int_0^{2 \pi} \kappa_n(\phi) \text{d} \phi = \frac{\kappa_1+\kappa_2}{2}\)
- Gaussian curvature \(K = \kappa_1 \cdot \kappa_2\)
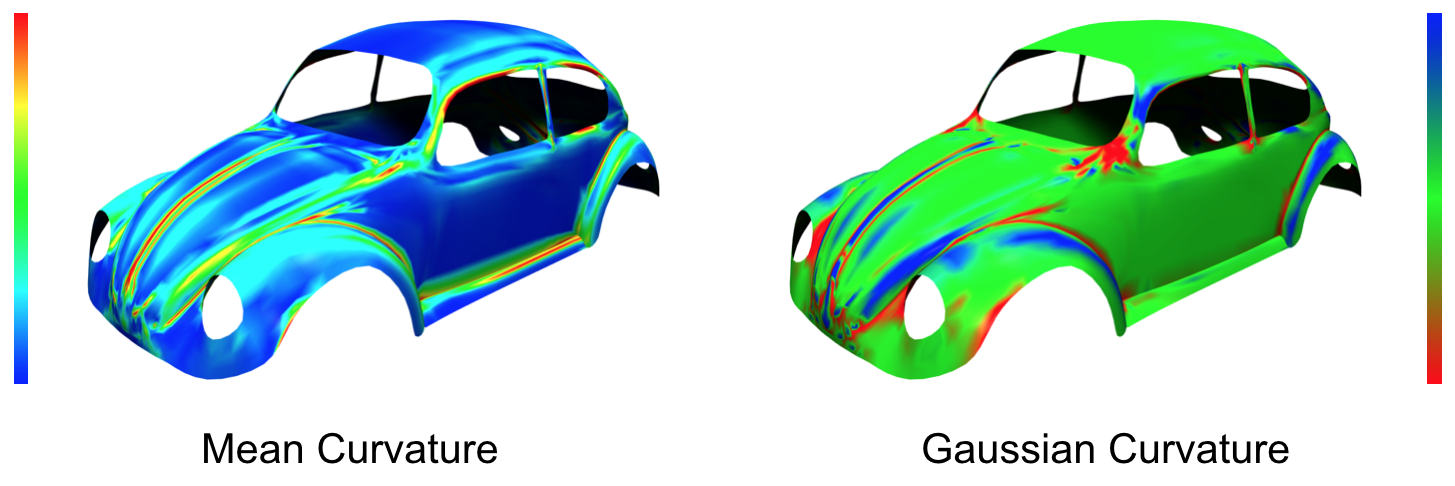
Classification
A point \(\vec{x}\) on the surface is called
- elliptic, if \(K > 0\)
- hyperbolic, if \(K < 0\)
- parabolic, if \(K = 0\)
- umbilic, if \(\kappa_1 = \kappa_2\)
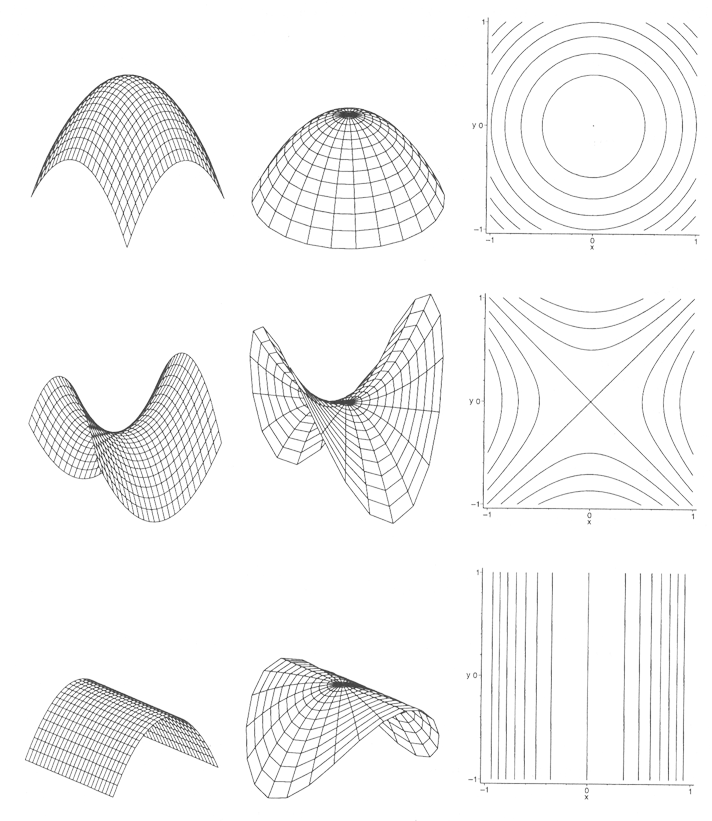
Surface Curvature(s)
Surface Curvature(s)
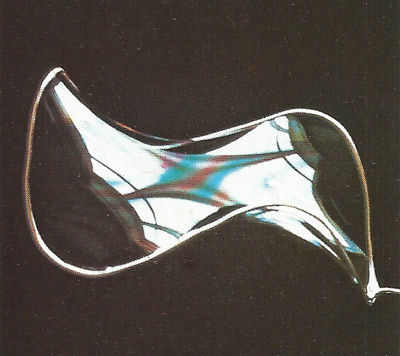
Minimal Surfaces
- Mean curvature \(H = \frac{\kappa_1 + \kappa_2}{2}\)
- \(H = 0\) everywhere → minimal surface
- all points must be hyperbolic (saddle points)
- Example: Soap films
Wikipedia: Minimal Surface Explanatory Movie
Minimal Surfaces
- Mean curvature \(H = \frac{\kappa_1 + \kappa_2}{2}\)
- \(H = 0\) everywhere → minimal surface
- all points must be hyperbolic (saddle points)
- Example: Sculpture



Developable Surfaces
- Gaussian curvature \(K = \kappa_1 \cdot \kappa_2\)
- \(K = 0\) everywhere → developable surface
- all points must be parabolic
Wikipedia: Developable Surface
Developable Surfaces
- Curved foldings


Theorema Egregium
Gaussian curvature only depends on lengths of surface curves, i.e., on the first fundamental form
\[ K(\vec{x}) = \lim_{r \to 0} \frac {6 \pi r - 3C_r(\vec{x})}{\pi r^3} \]
\(C_r(\vec{x})\) is the length of geodesic circle of radius \(r\) around \(\vec{x}\).
See this link for more ways to define/compute Gaussian curvature
Recap: Differential Operators
- Gradient \(\begin{eqnarray*} \nabla f := \left(\frac{\partial f}{\partial x_1}, \ldots, \frac{\partial f}{\partial x_n} \right) \end{eqnarray*}\)
- points in direction of steepest ascent
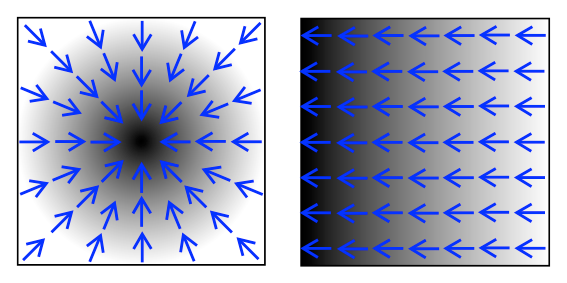
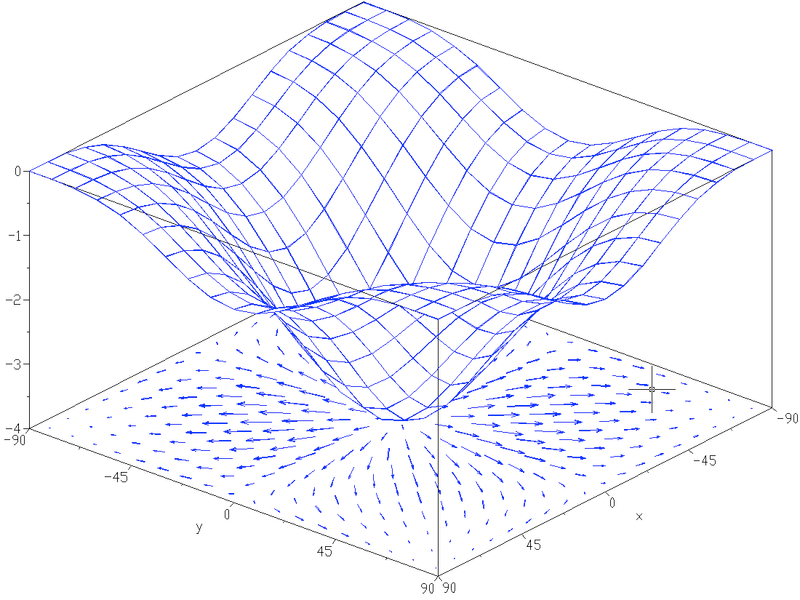
Wikipedia: Gradient
Recap: Differential Operators
- Divergence \(\begin{eqnarray*} \text{div} F = \nabla \cdot F := \frac{\partial F_1}{\partial x_1} + \ldots + \frac{\partial F_n}{\partial x_n} \end{eqnarray*}\)
- volume density of outward flux of vector field
- magnitude of source or sink at given point
Wikipedia: Divergence Khan Academy: Divergence
Recap: Laplace Operator
- Divergence of gradient of a function in \(\R^n\) \[ \laplace f \;=\; \grad \cdot \grad f \;=\; \sum_{i=1}^n \frac{\partial^2 f}{\partial x_i^2} \]
- Intuition: Laplacian measures difference to average in a local neighborhood
Wikipedia: Laplace Operator
Laplace-Beltrami Operator
- Extension of Laplace operator to functions \(f\) on manifolds \(\set{S}\): \[ \laplace_{\set{S}} f \;=\; \grad_{\set{S}} \cdot \grad_{\set{S}} f \]
- The operators \(\grad_{\set{S}}\cdot\) and \(\grad_{\set{S}}\) denote extensions of diverence and gradient to functions on manifolds.
- Laplace-Beltrami operator applied to the coordinate function \(\vec{x} \colon \set{S} \to \R^3\) gives mean curvature normal \[ \laplace_{\set{S}} \vec{x} = -2 \, H(\vec{x}) \, \vec{n}(\vec{x}) \]
- \(H\) and \(\vec{n}\) denote mean curvature and surface normal
- By discretzing Laplace-Beltrami we get the mean curvature
Wikipedia: Laplace-Beltrami Operator
Outlook
- Next time, we will
- see how to represent surfaces with triangle meshes
- discuss mesh data structures
- derive discrete versions of the curvature measures