Last Time: 3D Scanning Techniques
Last Time: Digital fabrication



- Fabrication technologies
- Subtractive
- Laser cutting
- CNC (computer numerical control) turning/milling
- Additive
- 3D printing
- Subtractive
- Designing parts for 3d printing
Overview
- Geometry Representations
- Implicit & parametric
- Continous & discrete
- Parametric curves
- Reparameterization
- Computing length
Geometry Representations
- How can we define a unit circle centered at the origin?
- In words: All points that are at distance one from the origin
Geometry Representations
- How can we define a unit circle centered at the origin?
- In words: All points that are at distance one from the origin
- Aside: How to compute distance between points \(\vec{x}, \vec{y} \in \R^n\)?
- \(dist(\vec{x}, \vec{y}) = \| \vec{x} - \vec{y} \|\), where \(\| \cdot \|\) defines a norm
- A norm on \(\R^n\) is a function \(\| \cdot \| : \R^n \mapsto \R\) with
- \(\| a \vec{x} \| = |a| \| \vec{x} \| \quad\) (homogeneity)
- \(\| \vec{x} + \vec{y} \| \leq \| \vec{x} \| + \| \vec{y} \| \quad\) (triangle inequality)
- \(\| \vec{x} \| \geq 0 \quad\) (positivity)
- If \(\| \vec{x} \| =0\), then \(\vec{x} = \vec{0} \quad\) (zero vector)
- we usually work with the Euclidean norm defined as \(\|\vec{x} \|_2 = \sqrt{x_1^2 + \cdots+ x_n^2}\)
Geometry Representations
- How can we define a unit circle centered at the origin?
- In words: All points that are at distance one from the origin
- Mathematically: \(\{ \vec{x} = (x,y) \in \R^2 \mid \sqrt{x^2 + y^2} = 1 \}\)
- Implicit Representation
- Kernel of function \(F : \R^n \mapsto \R\), i.e. \(\{\vec{x} \in \R^n \mid F(\vec{x}) = 0\}\)
- Unit Circle: \(F(x,y) = \sqrt{x^2 + y^2} - 1\)
- Circle of radius \(r\) centered at \((c_x, c_y)\): \[F(x,y) = \sqrt{(x-c_x)^2 + (y-c_y)^2} - r = 0\]
- Unit Sphere: \(F(x,y,z) = \sqrt{x^2 + y^2 + z^2} - 1\)
Implicit Representation
- Kernel of function \(F \colon \R^n \to \R\), i.e. \(\{\vec{x} \in \R^n \mid F(\vec{x}) = 0\}\)
- Notion of distance not crucial, only zero set is relevant
- Different functions \(F\) can yield the same geometry
- Example: Unit Circle: \(F(x,y) = \sqrt{x^2 + y^2} - 1\) or \(F(x,y) = x^2 + y^2 - 1\)
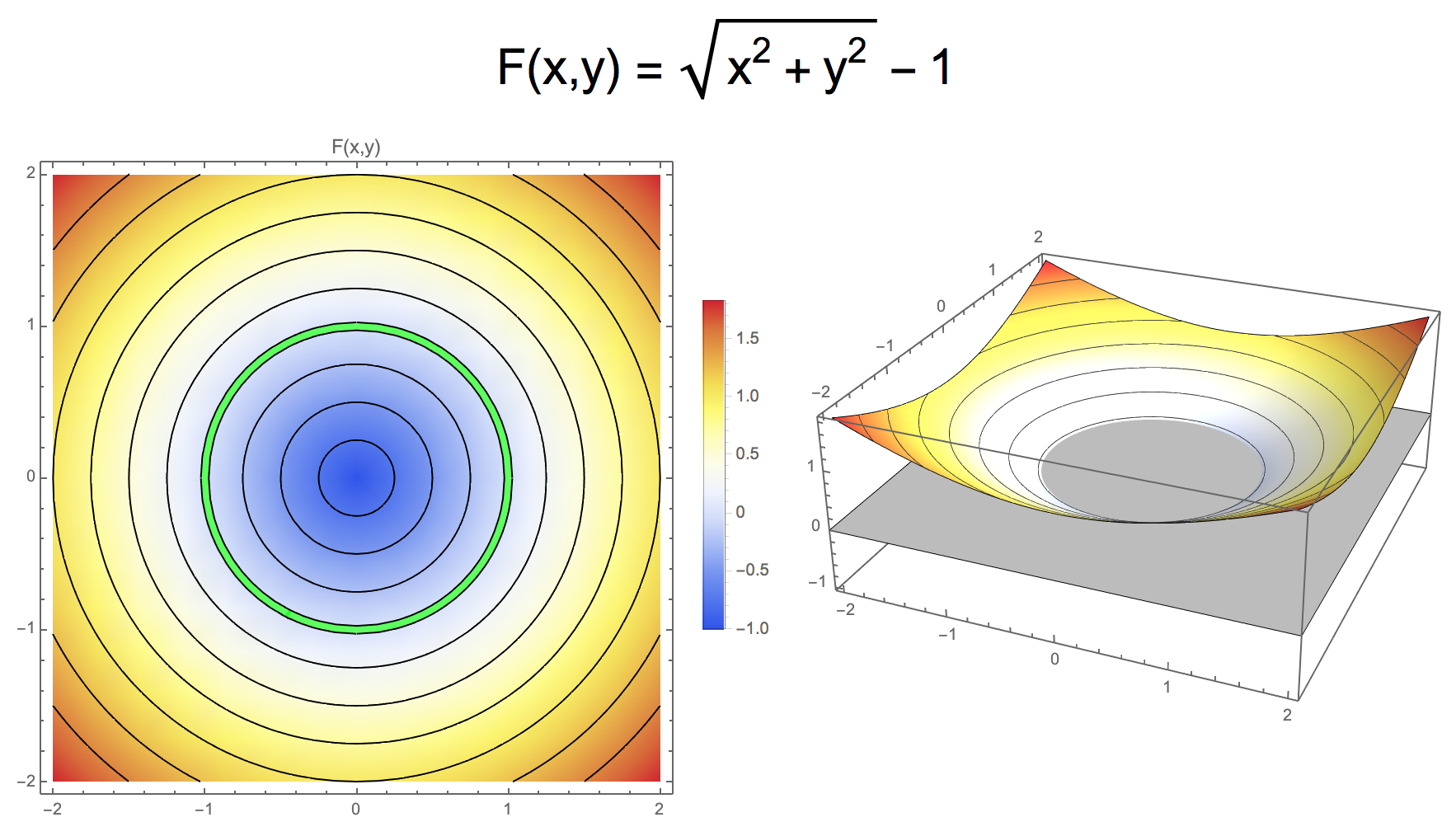
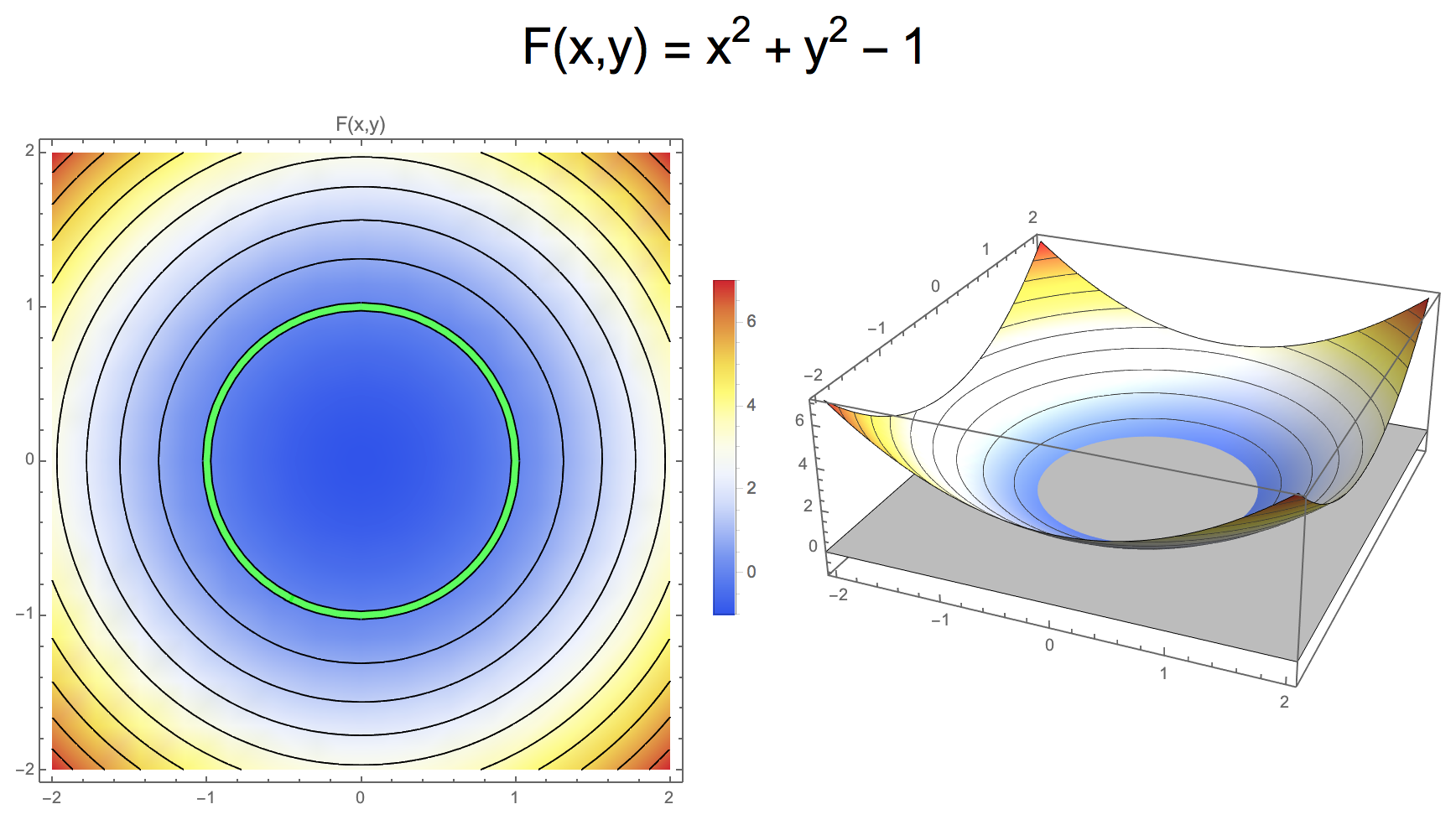
Implicit Representation
- Implicit function defines a closed surface at \(F(\vec{x}) = 0\) embedded in \(\R^n\) that separates space into inside and outside
- Typical convention for sign
- Interior: \(F(\vec{x}) < 0\)
- Exterior: \(F(\vec{x}) > 0\)

Implicit Curves
- Level set of 2D function defines 1D curve
- different level values define different curves
Implicit Surface
- Level set of 3D function defines 2D surface
Gradient of Implicit Function
- Gradient of function \(F : \R^n \mapsto \R\) is defined as \[\nabla F = \left[ \frac{\partial F}{\partial x_1} \; \frac{\partial F}{\partial x_2} \; \cdots \;\frac{\partial F}{\partial x_n} \right]^T\]
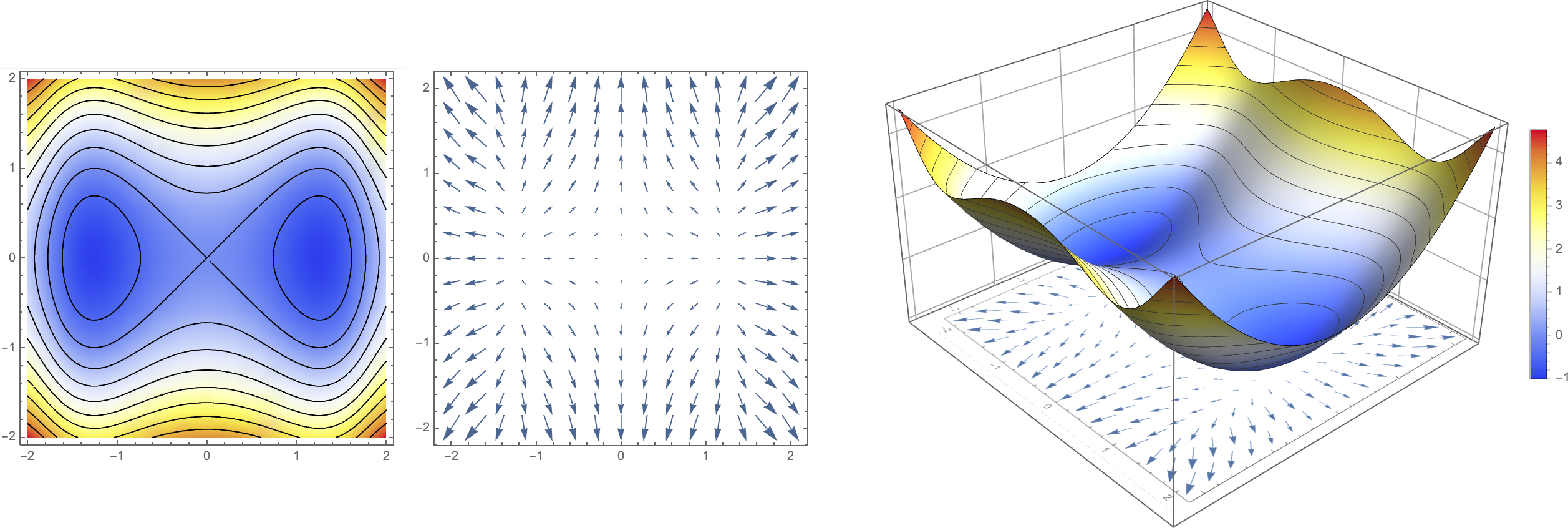
- \(\nabla F\) points into the direction of steepest ascent. Why?
Gradient of Implicit Function
- Gradient of function \(F : \R^n \mapsto \R\) is defined as
\[\nabla F = \left[ \frac{\partial F}{\partial x_1} \; \frac{\partial F}{\partial x_2} \; \cdots \;\frac{\partial F}{\partial x_n} \right]^T\]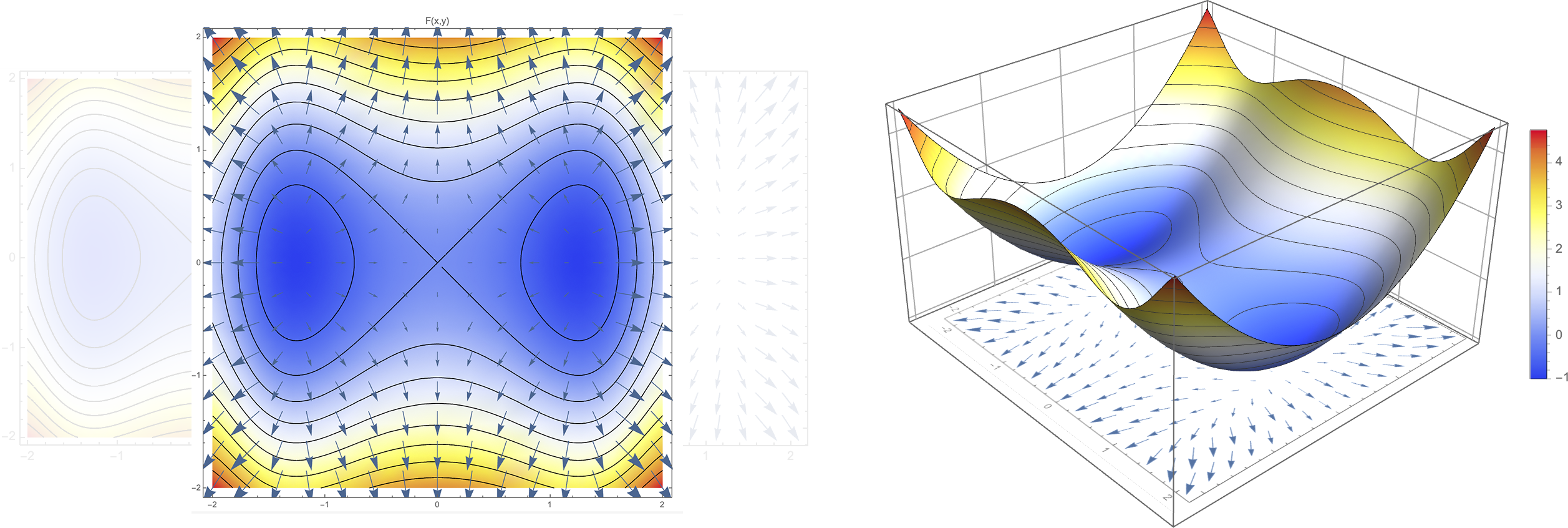
- Gradient \(\nabla F\) is orthogonal to level set
Signed Distance Function (SDF)
- Special case of an implicit representation
- \(F(\vec{x})\) gives signed distance to closest point on level surface
- \(\nabla F\) is unit surface normal
- level sets are at constant offset distance
- SDF of circle:
\[F(x,y) = \sqrt{x^2 + y^2} - 1\]
- SDF of sphere
\[F(x,y,z) = \sqrt{x^2 + y^2 + z^2} - 1\]
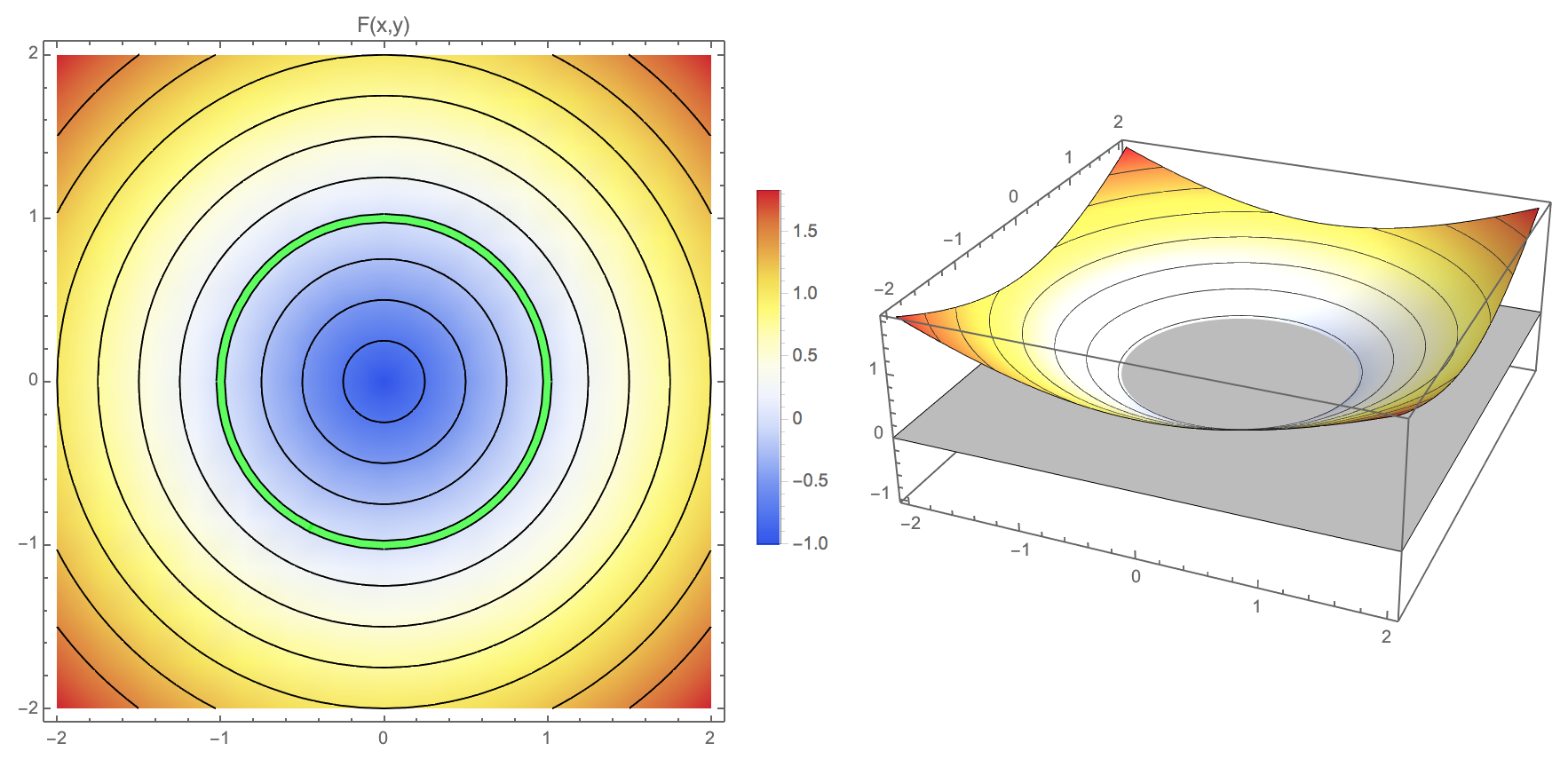
Modeling with Implicit Representations?
- Guess the shape of the curve!
\[F(x,y) = (y - \sqrt[3]{x^2})^2 + x^2 - 1\]
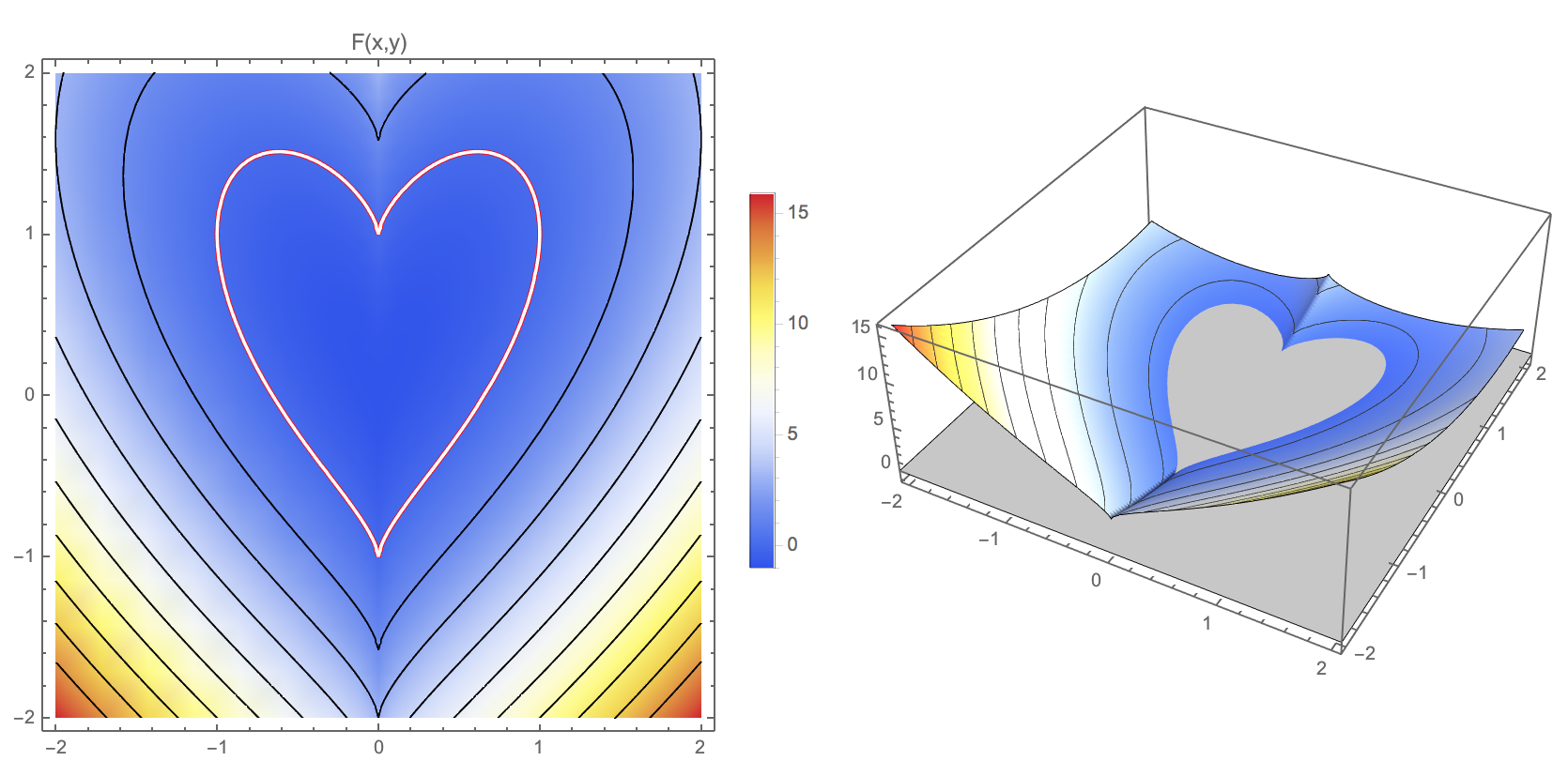
Modeling with Implicit Representations?
- Finding functions for a specific shape is not trivial
- What is an implicit function for this shape?
- Solution: Divide and conquer → piecewise representation
Discrete Implicit Representation
- An implicit function \(F\) can be discretized by sampling
- Reconstruct continuous function from discrete values
- Example:
Discrete Implicit Representation
- An implicit function \(F\) can be discretized by sampling
- Reconstruct continuous function from discrete values
- Example: Piecewise linear representation on regular grid
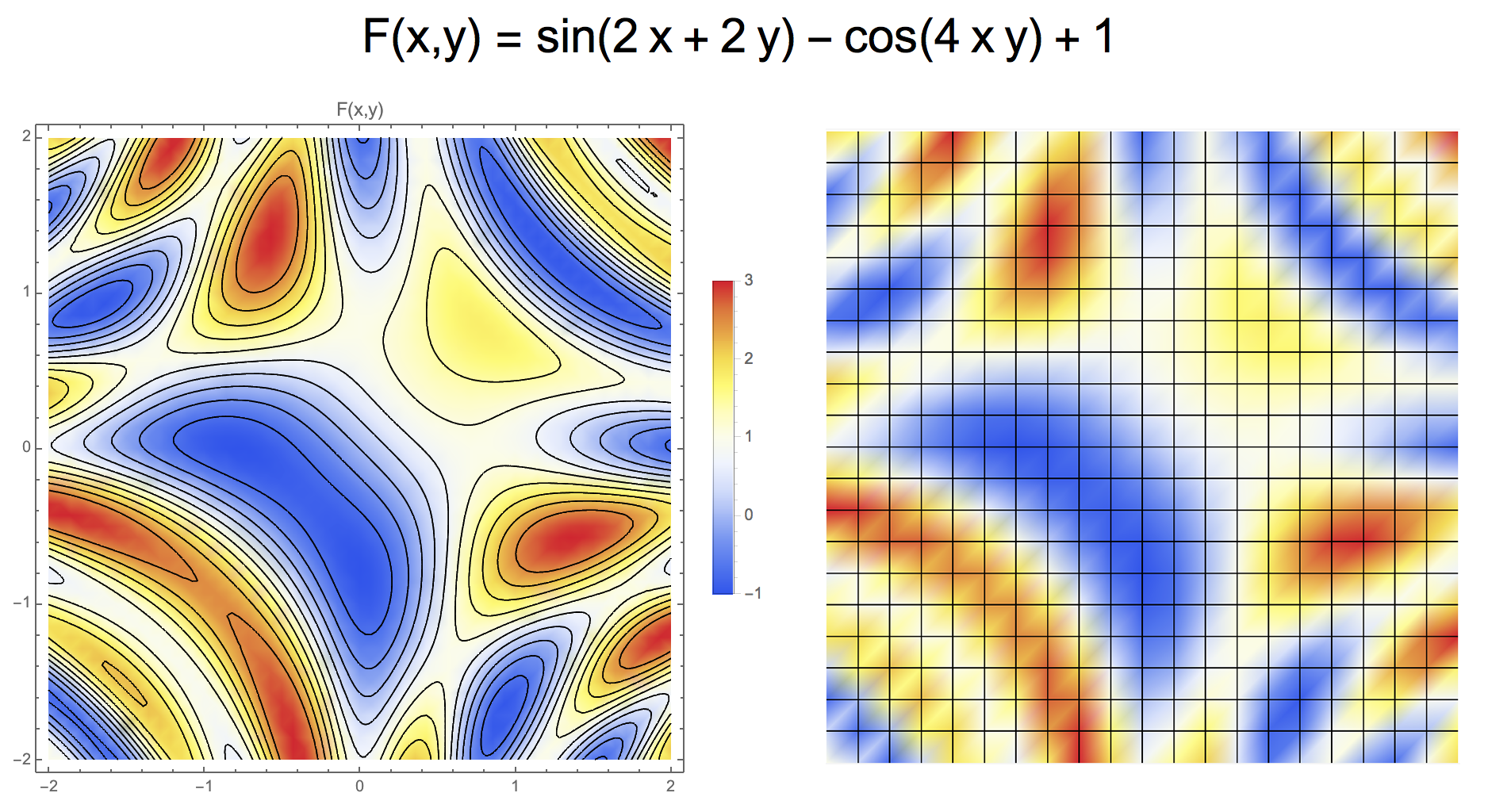
2D Marching Squares Algorithm
- Classify grid nodes as inside/outside
- Is \(F(x_{i,j})\) below or above iso-value?
- Classify cell: \(2^4 = 16\) configurations
- in/out for each corner
- Determine contour edges
- look-up table for edge configuration
- Determine vertex positions
- linear interpolation of grid values along edges
2D Marching Squares Algorithm
2D Marching Squares Algorithm
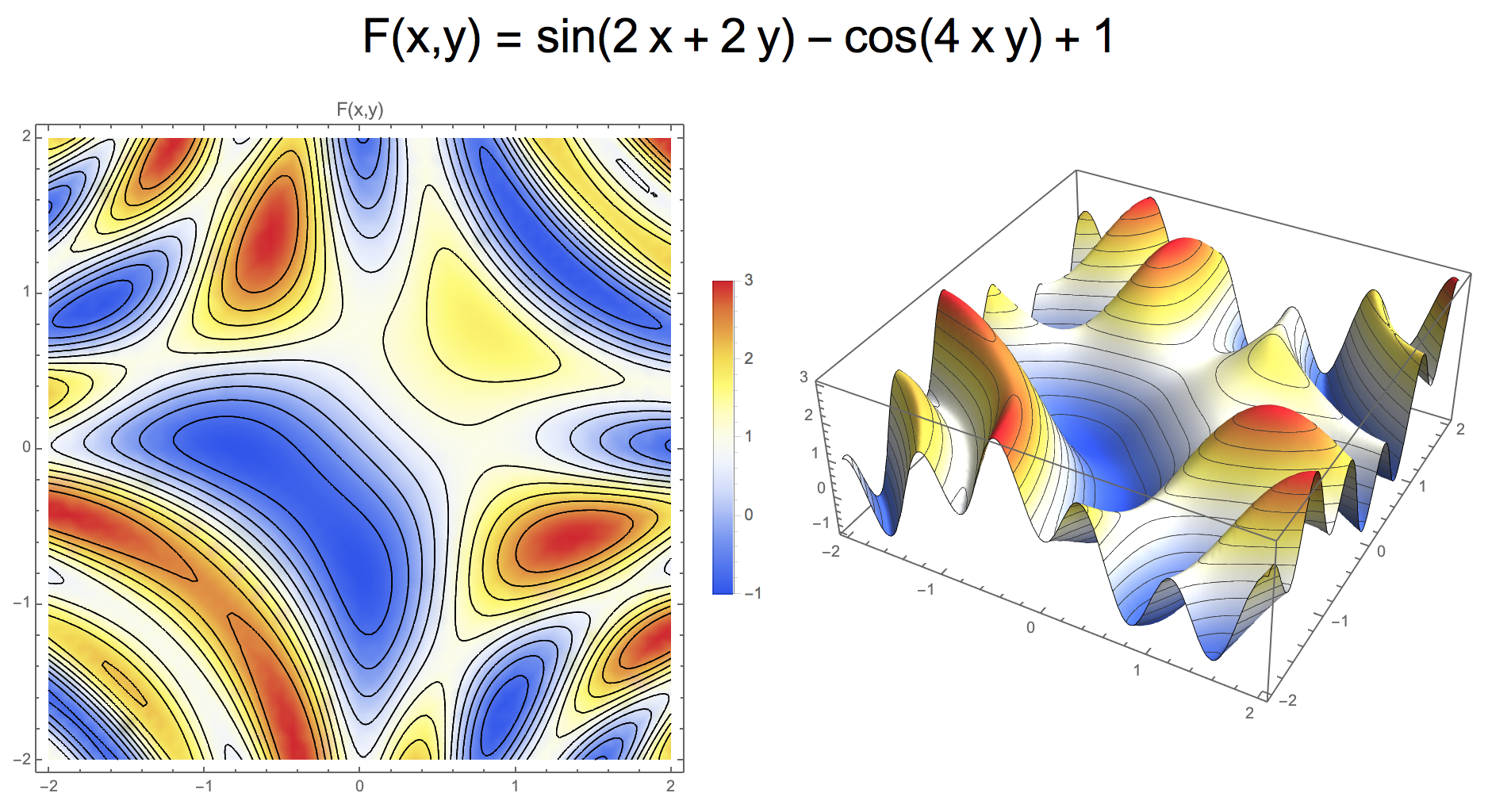
- Example: \(F(x,y) = \sin(2x +2y) - \cos(4 x y ) + 1 = 0\)
- Discretization implies loss of information!
- deviation particularly strong in regions of high curvature

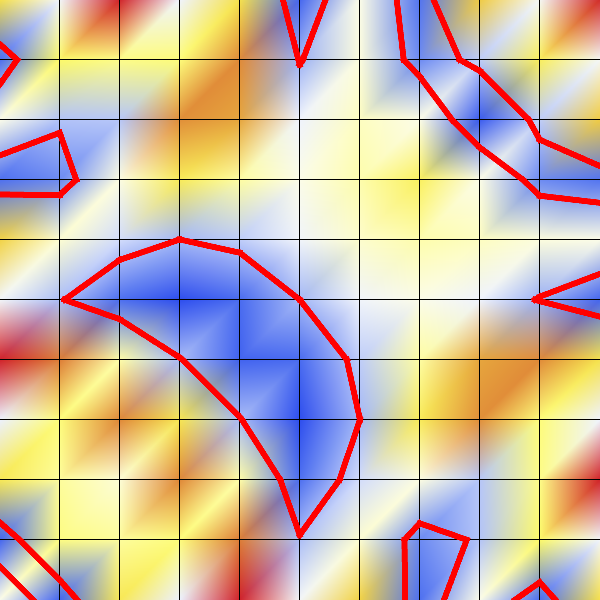
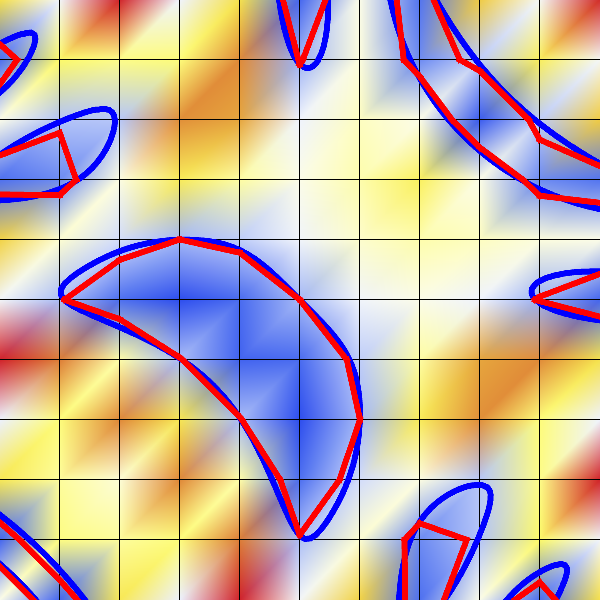
2D Marching Squares Algorithm
- Example: \(F(x,y) = \sin(2x +2y) - \cos(4 x y ) + 1 = 0\)
- Increasing resolution reduces reconstruction error
- Nyquist!

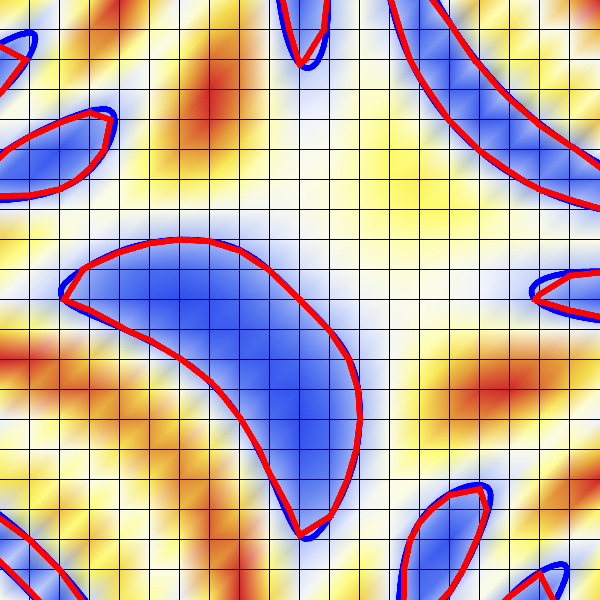
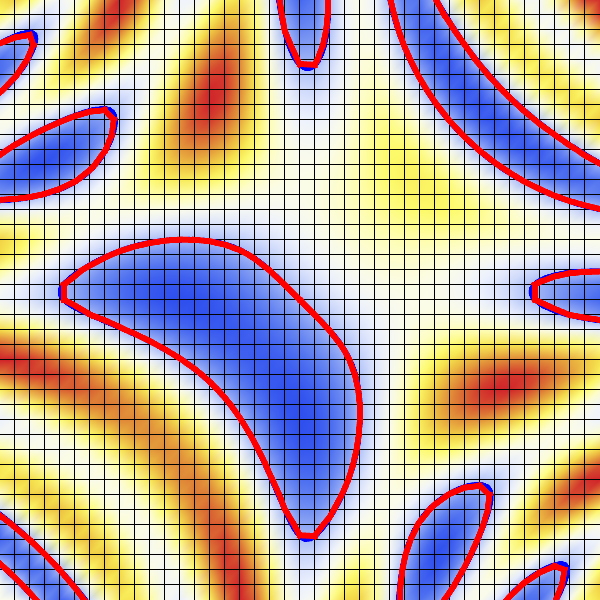
Discrete Implicit Representation
- How to define an implicit function for this shape?
- We can build a discrete implicit representation by computing the (signed) distance to the surface!
Implicit Switzerland
Implicit Switzerland

Implicit Switzerland
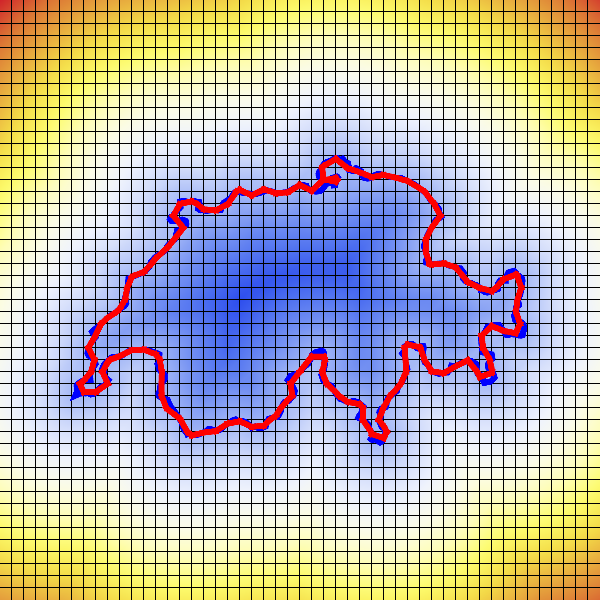
Implicit Switzerland
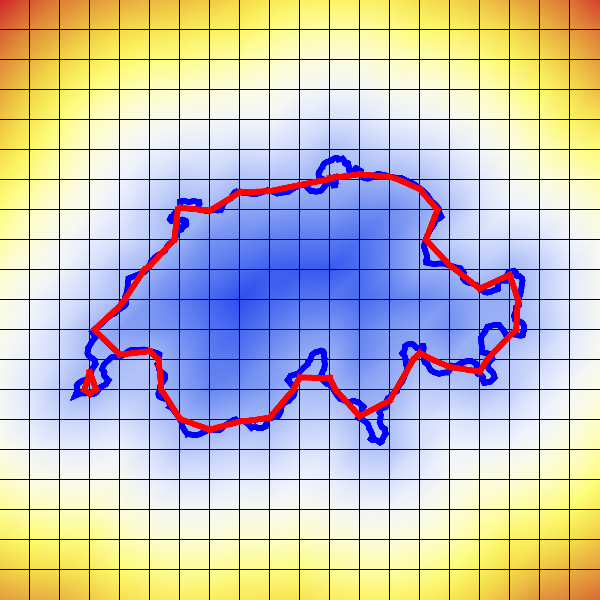
Implicit Representations
- Summary
- Kernel of function \(F \colon \R^n \to \R\), i.e. \(\{\vec{x} \in \R^n \mid F(\vec{x}) = 0\}\) defines closed surface, gradient \(\nabla F\) defines surface normal
- Signed Distance Function (SDF) as special case with unique properties
- Modeling with functions is hard → discrete representation
- Marching squares (cubes) to reconstruct level set from grid
- Pros
- Easy to determine if point is inside or outside (e.g. for collision detection)
- Easy to handle topology changes
- Cons
- Hard to generate points on surface (e.g. for rendering) or to modify geometry (e.g. deform surface)
Implicit Representations
- We will later see the how to use implicit representations to
- reconstruct surfaces from scanner data
- perform composition operations

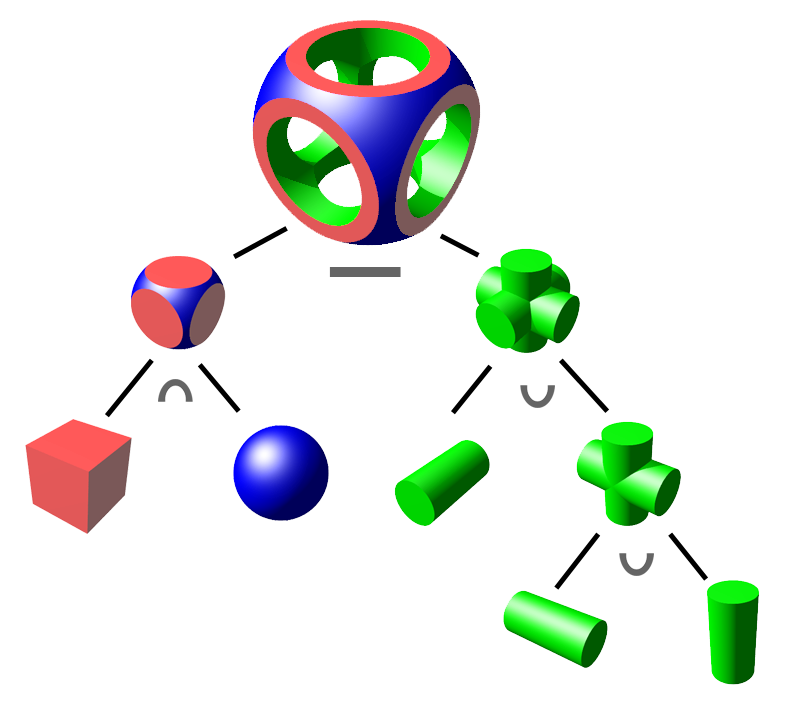
Parametric Representations
Geometry Representations
How can we define a unit circle centered at the origin?
Implicit Representation
Kernel of function \(F : \R^2 \mapsto \R\), i.e. \(\{\vec{x} \in \R^2 \mid F(\vec{x}) = 0\}\)
Unit Circle: \(F(x,y) = \sqrt{x^2 + y^2} - 1\) or \(F(x,y) = x^2 + y^2 - 1\)
Explicit (or Parametric)
Range of function \(\vec{x}: [a,b] \subset \R \mapsto \R^2\), i.e. \(\{\vec{x}(t) \mid t \in [a,b] \}\)
Unit Circle: \(\vec{x}(t) = \matrix{x(t) \\ y(t)} = \matrix{\cos(t) \\ \sin(t)}\), \(t \in [0, 2 \pi]\)
Parametric Representation
- Parametric representation \(\vec{x}: [a,b] \subset \R \mapsto \R^2\)
\[\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t}}\]
- Curve is defined as image of interval \([a,b]\) under parameterization function \(\vec{x}\).
Parametric Representation
- Parametric representation \(\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t}}\)
Parametric Representation
- Guess the shape of the curve!
\[\vec{x}\of{t} = \matrix{\sin^3(t) \\ \frac{1}{16}(13\cos(t) - 5 \cos(2t) - 2 \cos(3t)-\cos(4t))}\]
Parametric Representation
Parametric Curve Properties
- A parametric curve \(\vec{x}\of{t}\) is
- simple: \(\vec{x}\of{t}\) is injective (no self-intersections)
- differentiable: \(\vec{x}’\of{t}\) is defined for all \(t \in [a,b]\)
- regular: \(\vec{x}’\of{t} \neq \vec{0}\) for all \(t \in [a,b]\)
- Which of the following are simple, differentiable, regular?
Re-parameterization
- We can represent the same geometry with different parameter functions
- For example, the same curve is defined for \(t \in [0,1]\) by the functions \[\vec{x}_1\of{t} = \matrix{\sin(4 \pi t) \\ \cos(2 \pi t)}
\;\text{ and }\;
\vec{x}_2\of{t} = \matrix{\sin(4 \pi \sqrt{t}) \\ \cos(2 \pi \sqrt{t})}\]
- In other words, the image of \([0,1]\) under \(\vec{x}_1\) and \(\vec{x}_2\) is equivalent
- However: \(\vec{x}_1\of{t} \neq \vec{x}_2\of{t}\)!
Re-parameterization
- We can map from \(\vec{x}_1\) to \(\vec{x}_2\) using a re-parameterization function \(u\)
- In our example, we have \(u \colon [0,1] \to [0,1]\) with \(u(t) = \sqrt{t}\)
- If \(\vec{x}_1(t) = \vec{c}(t)\), then \(\vec{x}_2(t) = \vec{c}(u(t))\)
Re-parameterization
- We can map from \(\vec{x}_1\) to \(\vec{x}_2\) using a re-parameterization function \(u\)
- In our example, we have \(u \colon [0,1] \to [0,1]\) with \(u(t) = \sqrt{t}\)
- If \(\vec{x}_1(t) = \vec{c}(t)\), then \(\vec{x}_2(t) = \vec{c}(u(t))\)
- Parameter intervals do not need to be identical!
- For example, if \(\vec{x}_1 \colon [a,b] \to \R^2\) and \(\vec{x}_2 \colon [c,d] \to \R^2\) define the same curve, we can define a re-parameterization function \(u \colon [a,b] \to [c,d]\) such that \(\vec{x}_1(t) = \vec{x}_2(u(t))\)
Quiz
- Which of the following parametric curves have the same geometry as \(\trans{[ \cos(t), \sin(t)]}, t \in [0, \pi]\)?
Discrete Explicit Representation
Sample the parameter interval \([a,b]\), e.g., at parameters \(t_i = a + i \frac{b-a}{n},\; i = 0, \ldots, n\)
Then the polyline through the points \(\vec{x}\of{t_i}\) is a piecewise linear approximation of the curve \(\vec{x}\)
- With increasing \(n\), the polyline converges to the curve
Length of a Curve
- How can we measure length of a continuous curve?
- Example: What is the length of a parabola \(y = x^2\), \(x \in [0,1]\)?
- We know how to measure the length of a polyline!
- Let \(t_i = a + i \Delta t\) and \(\vec{x}_i = \vec{x}\of{t_i}\)
- Polyline chord length
\[ L_P = \sum_i \norm{ \Delta \vec{x}_i } \quad \quad \Delta\vec{x}_i := \norm{\vec{x}_{i+1} - \vec{x}_i} \]
Length of a Curve
- Polyline chord length
\[ L_P = \sum_i \norm{ \Delta \vec{x}_i } = \sum_i \norm{ \frac{\Delta \vec{x}_i}{\Delta t} } \Delta t \quad \quad \Delta\vec{x}_i := \norm{\vec{x}_{i+1} - \vec{x}_i} \]
- Curve arc length \((\Delta t \rightarrow 0)\)
\[ L = \int_a^b \norm{\vec{x}’} \mathrm{d}t = \int_a^b \sqrt{\left(\frac{\mathrm{d} x}{\mathrm{d} t} \right)^2 + \left( \frac{\mathrm{d} y}{\mathrm{d} t} \right)^2} \mathrm{d} t \]
Length of a Curve
- Example: Length of Circle
\[\vec{x}\of{t} = \matrix{\sin\of{t} \\ \cos\of{t}} \qquad \vec{x}’\of{t} = \matrix{\cos\of{t} \\ -\sin\of{t}}\]
\[ L \;=\; \int_a^b \norm{\vec{x}'(t)} \mathrm{d}t \;=\; \int_a^b \sqrt{\left(\frac{\mathrm{d} x(t)}{\mathrm{d} t} \right)^2 + \left(\frac{\mathrm{d} y(t)}{\mathrm{d} t} \right)^2} \mathrm{d} t \]
\[ L = \int_0^{2 \pi} \sqrt{\cos^2\of{t} + \sin^2\of{t}} \mathrm{d} t = \int_0^{2 \pi} 1 \mathrm{d} t = 2 \pi\]
Length of a Curve
- Example: Length of Parabola
\[\vec{x}\of{t} = \matrix{t \\ t^2}\]
\[\vec{x}’\of{t} = \matrix{1 \\ 2t}\]
\[ L = \int_0^1 \sqrt{1 + 4 t^2} \mathrm{d} t \]
\[ L = \frac{1}{4} (2 \sqrt{5} + \sinh^{-1}(2)) \approx 1.47894 \]
Outlook
- We can represent geometry with implicit or parametric functions
- We will see when which representation is preferable
- We will mostly work with parametric/explicit representations
- We will use discrete representations for geometry processing
- We will see how to extend polylines to polygonal meshes