Computer Graphics
Assignment 11 + 12 – Mock Exam and Animating the Camera Path
Martin Heistermann and Valentin
Wyss
Computer Graphics
Group
Assignment 12 (Bonus) + General info
- You need 50% of all exercise points
- Total: 10 points \(\times\) 11 regular exercises
- \(\implies\) 55 points
- Assignment 12:
- Sample exam tasks
- not graded
- Will be partially discussed in final lecture
- We recommend solving it before then
- If you are short on points to be admitted the exam, but would like to take it:
- Let us know, we can try to find an arrangement
Assignment 11
- Extract the Bézier control points of the control polygon.
- Evaluate a point on a piecewise Bézier curve.
- Evaluate the tangent of a piecewise Bézier curve.
- Make the spaceship move along the path with constant speed.
- Attach the eye to the spaceship.

Piecewise cubic Bézier curve
- C2 continuity.
- Special control polygon - its control points come from “A frame” construction.
- Extract control points for member Bézier curves.
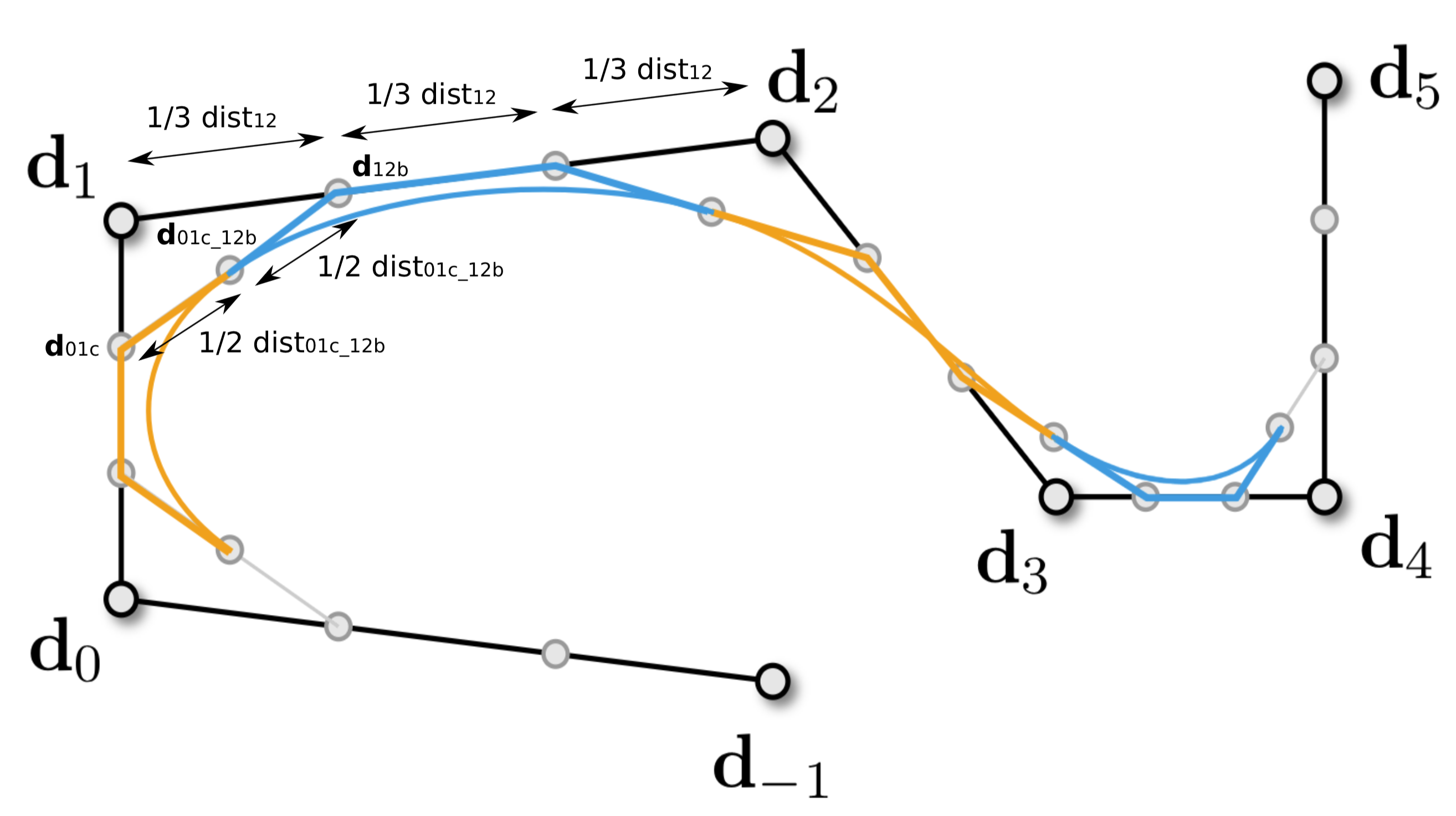
Evaluate points on a piecewise Bézier curve
- Parameter \(t \in [0, 1]\) traces the whole path.
- Scale it to parameter \(t'\in [0, 1]\) which traces a given Bézier segment.
- Standard de Casteljau algorithm.
Tangent of a piecewise Bézier curve
- Again, parameter \(t \in [0, 1]\) traces the whole path, map it to \(t'\) (do not forget the chain rule).
- Approach 1 - use DCA to evaluate quadratic Bézier Curve. \[ \frac{d \mathbf{c}(t)}{dt}=\sum_{i=0}^{n} \mathbf{b}_{i}\frac{dB^{n}_{i}(t)}{dt}=n \sum_{i=0}^{n-1}(\mathbf{b}_{i+1} - \mathbf{b}_{i})B^{n-1}_{i}(t) \]
- Approach 2 - Use the difference of the points from the last step of DCA
Ensure the constant velocity of the spaceship
- Linearly interpolating \(t\) and evaluating the path does not result in constant speed with constant time step \(dt\).
- We want \(ds\) to be constant, but \(ds=dt * v \neq const.\), since \(v \neq const.\)
- Counteract the effect of varying \(v\), compute it at each position on the path.
Make the eye follow the spaceship
- Compute the view matrix.
- The eye should overlook the spaceship from slightly above
- The spaceship should appear static w.r.t. screen (as in FPS)

Questions?