Computer Graphics

Bézier Curves I

Prof. Dr. David Bommes
Computer Graphics Group

Course Evaluation

  • Feedback possible till December 15th, 18:00
  • Please participate
  • Add additional comments
  • Link
images/qr_evaluation_2025.png

Last Time: Procedural Modeling

Procedural Techniques

  • Ubiquitous in graphics
    • texturing, modeling, animation, etc.

images/proc_texture.png images/proc_plants.png images/proc_terrain.png images/proc_motion.jpg

Procedural Approach

  • Why?
    • automatic generation on the fly
    • compact representations
    • infinite detail
    • unlimited extent
    • parametric control
  • Particularly suitable for models resulting from processes that are repeating, self-similar, or random
  • Challenges: artistic control, debugging, efficiency

Noise Functions

  • Function \(\mathbb{R}^n \to [-1, 1]\), where \(n = 1,2,3...\)
  • Desirable properties
    • No obvious repetition
    • Rotation invariance
    • band-limited
      • frequencies stay finite
      • more structure than white noise
    • efficient to compute
    • reproducible
  • Fundamental “primitive” or building block of most procedural synthesis approaches

Classic Perlin Noise (1980s)

  • Interpolate random gradients with Hermite interpolation
hermite_interpolation

Fractal Brownian Motion (fBm)

  • Spectral synthesis of noise function
    • Progressively smaller frequency
    • Progressively smaller amplitude
  • Typically Perlin noise is used
  • Each term in the summation is called an octave
  • Each octave typically doubles frequency and halves amplitude

images/procedural_modeling/fbm_octaves/FBm_octave1.png images/procedural_modeling/fbm_octaves/FBm_octave2.png images/procedural_modeling/fbm_octaves/FBm_octave3.png images/procedural_modeling/fbm_octaves/FBm_octave4.png

Fractal Dimension Example: Koch Curve

images/procedural_modeling/Koch_curve.svg

\[ \begin{aligned} D &= \frac{\log(N)}{\log(r)} \\ \end{aligned} \]

\[ \begin{aligned} \\ N &= 4 \\ r &= 3 \\ D &= \log(4)/\log(3) \\ &= 1.26185951... \end{aligned} \]

Multifractals

  • Fractal system which has a different fractal dimension in different regions
  • Heterogeneous fBM
    • Typical implementations don’t just spatially vary the \(H\) parameter
    • One strategy: scale higher frequencies in the summation by the value of the previous frequency.
    • Many possibilities: heterogenous terrain, hybrid multifractal, ridged multifractal
      • See the Texturing & Modeling book [Ebert et al.] for details

Heterogeneous fBm

images/procedural_modeling/self_similarity/terrain_multifractal_perlin_noise.png images/procedural_modeling/self_similarity/terrain_one_minus_perlin_noise.png images/procedural_modeling/self_similarity/terrain_worley_voronoi.png images/procedural_modeling/self_similarity/terrain_worly_voronoi_2.png images/procedural_modeling/self_similarity/terrain_domain_distortion.png images/procedural_modeling/self_similarity/terrain_distorted_one_minus_perline.png source: Ken Musgrave

Today: Bézier Curves

Overview

images/graphics-geometry.svg

Geometric Modeling

  • How did we model geometry so far?
    • Direct modeling: meshes (explicit), spheres, cylinders, planes (implicit)
    • Procedural modeling: L-Systems, Terrains, etc.
  • Now: Brief introduction to freeform curves
    • Applications in Graphics
      • Camera paths, animation curves, fonts, CAD design, blending, etc.

Example: Camera Path

Source

Example: Animation Curves

Maya Animation Tutorial

Example: Dassault’s CATIA

images/dassaults-CATIA.png

Literature

  • Farin: Curves and Surfaces for CAGD. A Practical Guide, Morgan Kaufmann, 2001
    • Chapters 4 & 5
images/farin.png

Requirements

  • Which properties are important for a geometry representation?
    • Approximation power
    • Efficient evaluation of positions & derivatives
    • Ease of manipulation
    • Ease of implementation

How to make LOVE?

images/tshirt-love.jpg
getdigital

But how to draw a heart? images/bezier-heart-2.svg

We have to understand parametric space curves!

Parametric Curve Representation

  • Parametric representation \(\vec{x} \colon [a,b] \subset \R \to \R^3\) (or \(\R^2\)) \[\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t} \\ z\of{t}}\]

  • Curve is defined as image of interval \([a,b]\) under parameterization function \(\vec{x}\).

Parametric Representation

  • Parametric representation \(\vec{x}\of{t} = \transpose{\left[ x\of{t} ,\, y\of{t} \right]}\)

Guess the shape of the curve!

\[\vec{x}\of{t} = \matrix{\sin^3(t) \\ \frac{1}{16}(13\cos(t) - 5 \cos(2t) - 2 \cos(3t)-\cos(4t))}\]

images/HeartCurveX.svg images/HeartCurveY.svg

Guess the shape of the curve!

Tangent Vector

  • Parametric curve representation \[\vec{x}\of{t} = \matrix{x\of{t} \\ y\of{t} \\ z\of{t}}\]
  • First derivative defines the tangent vector \[\vec{t} = \vec{x}’\of{t} := \frac{\mathrm{d} \vec{x}\of{t}}{\mathrm{d} t} = \matrix{ \mathrm{d}x\of{t} / \mathrm{d} t \\ \mathrm{d}y\of{t} / \mathrm{d} t \\ \mathrm{d}z\of{t} / \mathrm{d} t}\]

Tangent Vector

  • Example: \(\vec{x}\of{t} = (1+\cos(t)) \matrix{\cos(t) \\ \sin(t)}\)

Discrete Curves

  • Approximate the curve by a polygon, e.g. for rendering
    1. Sample parameter interval: \(t_i = a + i\Delta t\)
    2. Sample curve: \(\textbf{x}_i = \textbf{x}(t_i)\)
    3. Connect samples by polygon

images/curve-approximation.svg

images/curve-approximation-ruler.svg

Polynomial Curves

\[ \vec{x}(t) = \sum_{i=0}^n \vec{b}_i \, \phi_i(t) \;\in \Pi^n\]

  • Ingredients
    • Vector-valued coefficients \(\vec{b}_i \in \R^3\)
    • Scalar-valued polynomials \(\phi_i \colon \R \rightarrow \R\)
    • \(\{ \phi_0, \ldots, \phi_n \}\) span space of degree \(n\) polynomials
  • Why polynomials?
    • Can be computed efficiently on a computer (only multiplications and additions needed)
    • Can approximate arbitrary functions (Weierstrass approximation theorem)
images/Karl-Weierstrass.png
Karl Weierstrass,
1815-1897

Polynomial Curves

Which basis functions \(\{ \phi_0, \ldots, \phi_n \}\) that span \(\Pi^n\), the space of polynomials of degree \(n\), should we use?

  • The monomial basis \(\{ t^0, t^1, \ldots, t^n \}\)?
  • Simple sum of points \(\vec{x}(t) = \sum_{i=0}^n \vec{b}_i \, t^i\) does not make sense
  • Coefficients \(\vec{b}_i\) have no geometric meaning
  • No intuitive curve manipulation

Monomial Basis

Check requirements for geometry representation:

  • Approximation power ✓
  • Efficient evaluation of positions & derivatives ✓
  • Ease of manipulation ✗
  • Ease of implementation ✓

Let’s find another basis of \(\Pi^n\)!

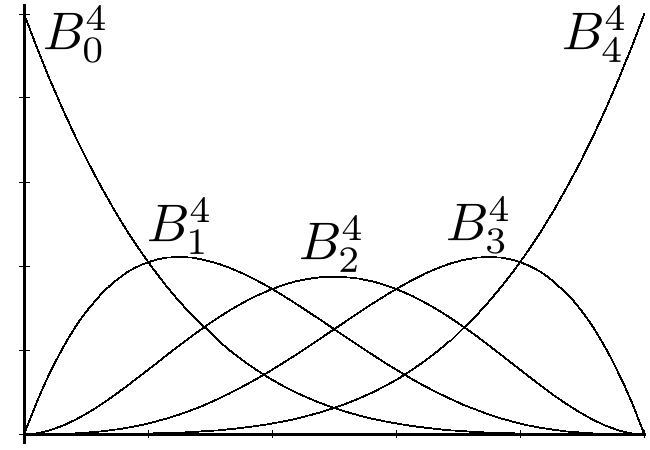
Bernstein Polynomials

\[ \begin{align*} B_i^n(t) &\;=\; \binom{n}{i} t^i (1-t)^{n-i} \,,\quad 0 \leq i \leq n\\ \binom{n}{i} &\;=\; \begin{cases} \frac{n!}{i!(n-i)!} & \text{if }0 \leq i \leq n, \\ 0 & \text{otherwise.} \end{cases} \end{align*} \]

images/bernstein-polynomials.png
images/Bernstein-sergei.png
Sergei Bernstein,
1880-1968

Bernstein Polynomials

\[B_i^n(t) = \binom{n}{i} t^i (1-t)^{n-i}\]

images/bernstein-polynomials.png

  • Basis: \(\{ B_0^n, \ldots, B_n^n \}\) are a basis for \(\Pi^n\)
  • Non-negativity: \(B_i^n(t) \geq 0\) for \(t \in [0,1]\)
  • Endpoints: \(B_i^n(0) = \delta_{i,0}\) and \(B_i^n(1) = \delta_{i,n}\)
  • Symmetry: \(B_i^n(t) = B_{n-i}^n(1-t)\)
  • Maximum: \(B_i^n(t)\) has maximum at \(t=i/n\).
  • Partition of unity: \(\sum_{i=0}^n B_i^n(t) = 1\)

Partition of Unity

Partition of unity: \(\sum_{i=0}^n B_i^n(t) = 1\)

Prove it!

\[ \begin{eqnarray*} 1 &=& t + (1-t) \\ &=& \left[ t + (1-t) \right]^n \\ &=& \sum_{i=0}^n \binom{n}{i} t^i (1-t)^{n-i} \\ &=& \sum_{i=0}^n B_i^n(t) \end{eqnarray*} \]

Bezier Curves

Bezier curves use Bernstein polynomials as basis: \[\vec{x}(t) = \sum_{i=0}^n \vec{b}_i \, B_i^n(t)\]

images/bezier-pierre.png
Pierre Bézier,
1910-1999

  • Coefficients \(\vec{b}_i\) are called control points
  • Points \(( \vec{b}_0, \ldots, \vec{b}_n )\) define the control polygon.

Properties of Bezier Curves

\[\vec{x}(t) = \sum_{i=0}^n \vec{b}_i \, B_i^n(t)\]

  • Affine combination: Point \(\vec{x}(t)\) is an affine combination of control points. Control points have a geometric meaning!
  • Follows from partition of unity of Bernstein basis

Properties of Bezier Curves

\[\vec{x}(t) = \sum_{i=0}^n \vec{b}_i \, B_i^n(t)\]

  • Convex hull: Curve \(\vec{x}(t)\) lies in convex hull of control points
  • Follows from partition of unity and non-negativity of Bernstein basis

Properties of Bezier Curves

\[\vec{x}(t) = \sum_{i=0}^n \vec{b}_i \, B_i^n(t)\]

  • Endpoint interpolation: Curve \(\vec{x}(t)\) starts at \(\vec{b}_0\) and ends at \(\vec{b}_n\).
  • Follows from \(B_i^n(0) = \delta_{i,0}\) and \(B_i^n(1) = \delta_{i,n}\).

Properties of Bezier Curves

\[\vec{x}(t) = \sum_{i=0}^n \vec{b}_i \, B_i^n(t)\]

  • Symmetry: Curve defined by \((\vec{b}_n, \vec{b}_{n-1}, \ldots, b_0)\) is the same as the one defined by \((\vec{b}_0, \vec{b}_1, \ldots, \vec{b}_n)\), just in reverse order.
  • Follows from symmetry of Bernstein basis

Properties of Bezier Curves

\[\vec{x}(t) = \sum_{i=0}^n \vec{b}_i \, B_i^n(t)\]

  • Pseudo-local control: Control point \(\vec{b}_i\) has its maximum effect on the curve at \(t=i/n\).
  • Follows from maxima of Bernstein polynomials.

Bezier Curves

Check requirements for geometry representation:

  • Approximation power ✓
  • Efficient evaluation of positions & derivatives ???
  • Ease of manipulation ✓
  • Ease of implementation ???

How to efficiently implement binomial coefficient and faculty?

\[ B_i^n(t) = \binom{n}{i} t^i (1-t)^{n-i} \quad\text{and}\quad \binom{n}{i} \;=\; \begin{cases} \frac{n!}{i!(n-i)!} & \text{if }0 \leq i \leq n, \\ 0 & \text{otherwise.} \end{cases} \]

de Casteljau Algorithm

  • Given:
    • Control polygon \(\vec{b}_0,\ldots,\vec{b}_n\)
    • Curve parameter \(t\)
  • Initialization: \(\vec{b}_i^0 = \vec{b}_i \quad i=0, \ldots, n\)
images/deCasteljau.jpg
Paul de Casteljau,
*1930
  • Recursion: \[ \vec{b}_i^k = (1-t)\,\vec{b}_i^{k-1} + t\,\vec{b}_{i+1}^{k-1} \] where \(k = 1,\ldots,n\) and \(i = 0,\ldots,n-k\)
  • Result: \(\vec{b}_0^n = \sum_{i=0}^n \vec{b}_i B_i^n(t) = \vec{x}(t)\)
images/successive-linear-interpolation.svg

Geometric Interpretation

images/successive-linear-interpolation.svg
image/svg+xml

de Casteljau \(\leftrightarrow\) Bernstein Basis

image/svg+xml

\[\begin{align*} \vec{b}_0^1 & = (1-t) \, \vec{b}_0 + t \, \vec{b}_1 \\ \vec{b}_1^1 & = (1-t) \, \vec{b}_1 + t \, \vec{b}_2 \\[3mm] \vec{b}_0^2 & = (1-t) \, \vec{b}_0^1 + t \, \vec{b}_1^1 \\ & = \underbrace{(1-t)^2}_{B_0^2(t)} \, \vec{b}_0 + \underbrace{2(1-t)t}_{B_1^2(t)} \, \vec{b}_1 + \underbrace{t^2}_{B_2^2(t)} \, \vec{b}_2 \end{align*}\]

Bernstein Recursion

Bernstein polynomials can be evaluated through a recursion:

\[B_i^n(t) = (1-t)\,B_i^{n-1}(t) \;+\; t\,B_{i-1}^{n-1}(t)\]

with \(B_0^0(t) = 1\) and \(B_i^n(t) = 0\) for \(i \notin \{0,\ldots,n\}\)

Prove it!

\[\begin{eqnarray*} B_i^n(t) &=& \binom{n}{i} t^i (1-t)^{n-i} \\[2mm] &=& \binom{n-1}{i} t^i (1-t)^{n-i} \;+\; \binom{n-1}{i-1} t^i (1-t)^{n-i} \\[2mm] &=& (1-t) \cdot \binom{n-1}{i} t^i (1-t)^{(n-1)-i} \;+\; t \cdot \binom{n-1}{i-1} t^{i-1} (1-t)^{(n-1)-(i-1)} \\[2mm] &=& (1-t)\,B_i^{n-1}(t) \;+\; t\,B_{i-1}^{n-1}(t) \end{eqnarray*}\]

de Casteljau Construction

\[\begin{eqnarray*} \sum_{i=0}^n \vec{b}_i B_i^n(t) &=& \sum_{i=0}^n \vec{b}_i \left[ (1-t)\,B_i^{n-1}(t) \;+\; t\,B_{i-1}^{n-1}(t) \right] \\ &=& \sum_{i=0}^{n-1} \left[ (1-t)\,\vec{b}_i \;+\; t\,\vec{b}_{i+1} \right] \, B_{i}^{n-1}(t) \end{eqnarray*}\]

images/de-Casteljau-proof.svg

Try it yourself!

Applications of Bezier Curves

Bezier curves are the most prominent curve representation:

  • Used for 2D vector drawing applications
  • Used for 3D computer-aided design (CAD)
  • Used for true-type fonts

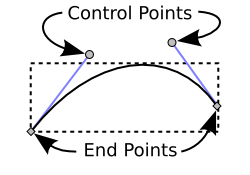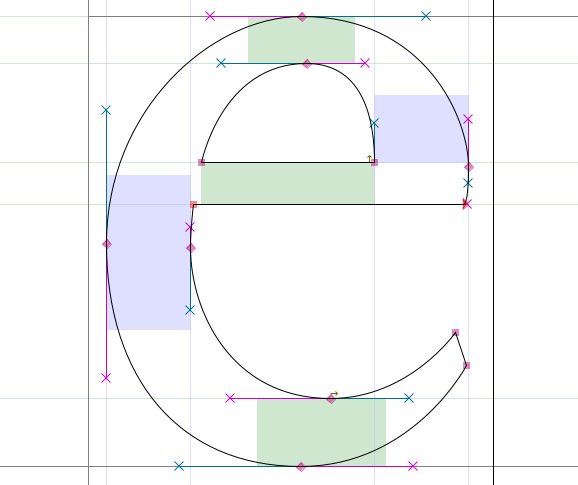images/inkscape-bezier-1.pngInkscape images/dassaults-CATIA.pngDassault CATIA images/fontforge.pngFontForge

Applications of Bezier Curves

image/svg+xml

Literature

  • Farin: Curves and Surfaces for CAGD. A Practical Guide, Morgan Kaufmann, 2001
    • Chapters 4 & 5
images/farin.png