Computer Graphics
Triangle Meshes
Last Time: Lighting
 no illumination
no illumination  local illumination
local illumination  global illumination
global illumination
Phong Lighting Model
- Ambient lighting
- approximate global light transport / exchange
- uniform in, uniform out

- Diffuse lighting
- dull / matt surfaces
- directed in, uniform out

- Specular lighting
- shiny surfaces
- directed in, directed out

Phong Lighting Model
 ambient: \(I_a m_a\)
ambient: \(I_a m_a\)  diffuse: \(I_l m_d \left( \vec{n} \cdot \vec{l} \right)\)
diffuse: \(I_l m_d \left( \vec{n} \cdot \vec{l} \right)\)  specular: \(I_l m_s \left( \vec{r} \cdot \vec{v} \right)^s\)
specular: \(I_l m_s \left( \vec{r} \cdot \vec{v} \right)^s\)

\[ I \;=\; I_a m_a + I_l \left( m_d \left( \vec{n} \cdot \vec{l} \right) + m_s \left( \vec{r} \cdot \vec{v} \right)^s \right) \]
Real or Rendered?







Fake Images and Videos
Today: Ray Tracing Meshes
- Extend ray tracing to triangle meshes
- Mesh data structures
- Lighting computations
- Efficient ray intersections
Triangle Meshes
What is a triangle mesh?
- Connectivity / Topology
- Vertices \(\mathcal{V} = \{ v_1, \dots, v_n \}\)
- Edges \(\mathcal{E} = \{ e_1, \dots, e_k \}\), \(e_i \in \mathcal{V} \times \mathcal{V}\)
- Faces \(\mathcal{F} = \{ f_1, \dots, f_m \}\), \(f_i \in \mathcal{V} \times \mathcal{V} \times \mathcal{V}\)
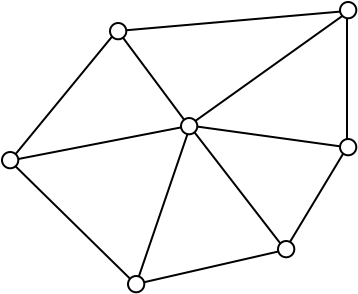
- Geometry
- Vertex positions \(\{ \vec{p}_1, \dots, \vec{p}_n \}\), \(\vec{p}_i \in \R^3\)
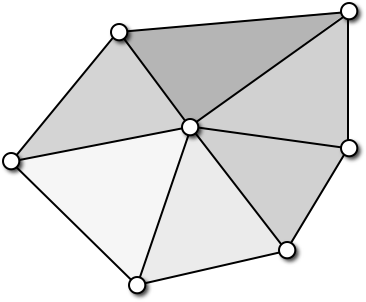
Triangle Meshes
- Triangle meshes can represent arbitrary surfaces

Triangle Meshes
- Triangle meshes can represent arbitrary surfaces
- Piecewise linear approximation → error is \(\mathcal{O}(h^2)\)
Triangle Meshes
- Triangle meshes can represent arbitrary surfaces
- Piecewise linear approximation → error is \(\mathcal{O}(h^2)\)
- Approximation error inversely proportional to #triangles
Triangle Meshes
- Triangle meshes can represent arbitrary surfaces
- Piecewise linear approximation → error is \(\mathcal{O}(h^2)\)
- Approximation error inversely proportional to #triangles
- Adaptive tesselation can adapt to surface curvature
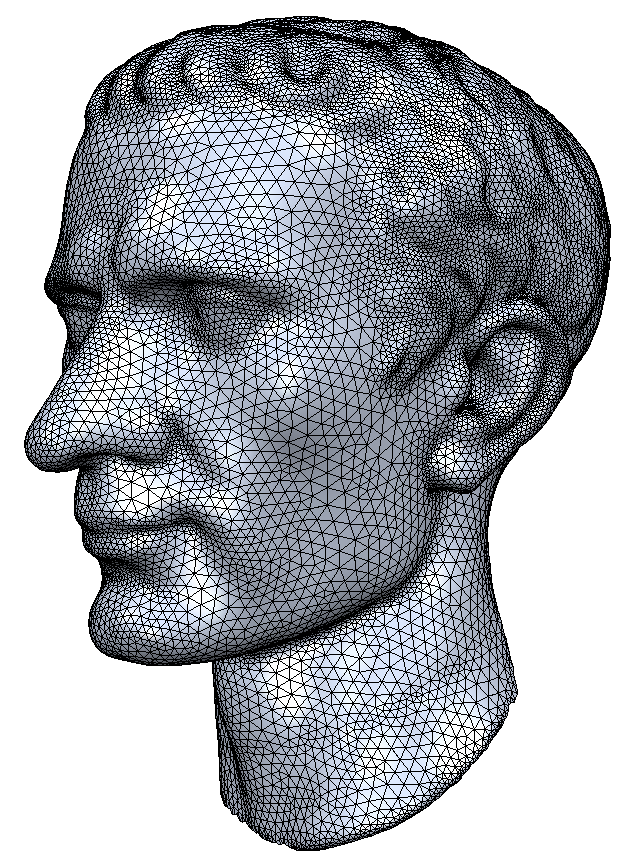 adaptive meshing
adaptive meshing  curvature visualization
curvature visualization
Triangle Meshes
- Triangle meshes can represent arbitrary surfaces
- Piecewise linear approximation → error is \(\mathcal{O}(h^2)\)
- Approximation error inversely proportional to #triangles
- Adaptive tesselation can adapt to surface curvature
- Simple primitives can be processed efficiently by CPU/GPU

Example: Stanford Bunny
- Observation:
- roughly twice as many faces as vertices
- roughly three times as many edges as vertices
- Coincidence?
- No!
- Euler Formula for meshes of genus 0 \[V - E + F = 2\]
- more on this in the course 3D Geometry Processing (spring)

Mesh Data Structures
Face Set
- Face Set is a standard file format for triangle meshes (e.g. STL format)
- Memory consumption
36 B/f = 72 B/v- recall: ~twice as many faces as vertices
Indexed Face Set
- Indexed Face Sets are used for many file formats (e.g. OFF, OBJ, VRML)
- Memory consumption
12 B/v + 12 B/f = 36 B/v
Face-Based Connectivity
- Store connectivity per face
- Memory consumption
16 B/v + 24 B/f = 64 B/v - Non-constant element size for general polygonal meshes
- Edges not represented
Edge-Based Connectivity
- Store connectivity per edge
- Memory consumption
16 B/v + 4 B/f + 32 B/e = 120 B/v - Edges explicitly represented
- Missing edge orientation leads to case distinctions during traversal
Halfedge-Based Connectivity
- Store connectivity per halfedge
- Memory consumption
16 B/v + 4 B/f + 20 B/h = 144 B/v
(can be reduced to 96 B/v) - Edges & halfedges explicitly represented
- No case distinctions during traversal!
One-Ring Traversal
- Simple one-ring traversal without case distinctions:
- Start at vertex
- Outgoing halfedge
- Opposite halfedge
- Next halfedge
- Opposite halfedge
- Next halfedge
- …
Half-Edge navigation demo
Halfedge-Based Libraries
- CGAL
- https://www.cgal.org
- Computational geometry
- OpenMesh
- https://www.openmesh.org
- Mesh processing
- Polygon Mesh Processing Library
Lighting & Shading
Ray Tracing Meshes
 We want this…
We want this…  …but we get this
…but we get this
Flat Shading vs. Phong Shading
- Flat shading
- Use constant face normal for lighting
- Yields facetted appearence
- Mach band effect emphasizes this even more

 Mach band effect
Mach band effect  source Wikipedia
source Wikipedia
Flat Shading vs. Phong Shading
- Flat shading
- Use constant face normal for lighting
- Yields facetted appearence
- Mach band effect emphasizes this even more

- Phong shading
- Use smooth normal field for lighting
- Compute normal vectors per vertex
- Barycentric interpolation of normal vectors

Normal Vectors
- Triangle normal
\[ \vec{n}(T) = \frac{\left(\vec{b}-\vec{a}\right) \times \left(\vec{c}-\vec{a}\right)} {\norm{\left(\vec{b}-\vec{a}\right) \times \left(\vec{c}-\vec{a}\right)}} \]
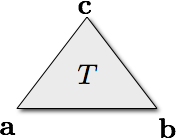
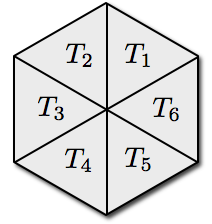
- Vertex normal
- Average of incident triangles’ normals \(\vec{n}(T_i)\)
- Weighted by area or opening angle \(w(T_i)\)
\[ \vec{n}(V) = \frac{ \sum_{T_i \ni V} w(T_i) \, \vec{n}(T_i)} { \norm{ \sum_{T_i \ni V} w(T_i) \, \vec{n}(T_i)} } \]
Vertex Normals
 triangulation (flat shading)
triangulation (flat shading)  no weighting
no weighting  angle-weighted
angle-weighted
Interpolate Vertex Normals
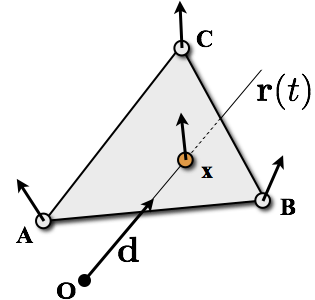
- Intersection point with barycentric coordinates \[ \vec{x} = \alpha\vec{A} + \beta\vec{B} + \gamma\vec{C}\]
- Linearly interpolate vertex normals \[ \vec{n}\of{\vec{x}} = \alpha\vec{n}\of{\vec{A}} + \beta\vec{n}\of{\vec{B}} + \gamma\vec{n}\of{\vec{C}} \]
- Use \(\vec{n}(\vec{x})\) to light point \(\vec{x}\)
- Normalize for lighting calculations!
Ray Tracing Meshes
 Flat Shading
Flat Shading  Phong Shading
Phong Shading
Ray Tracing Meshes
 Flat Shading
Flat Shading  Phong Shading
Phong Shading
Efficient Ray-Mesh Intersections
Ray-Mesh Intersections
- Brute-Force
- Intersect ray with all \(n\) mesh triangles
- Select intersection with smallest positive ray parameter \(t\)
- Computational cost: \(\mathcal{O}(n)\) for single ray
- Many unnecessary ray-triangle intersection tests

Spatial Data Structures
- Improve efficiency of ray-surface intersections by pre-sorting of primitives → spatial data structures
- Tradeoffs
- Applicability
- Performance
- Resources
- Implementation
- Examples
- uniform grids, adaptive grids, kd-trees, bsp-trees, bounding volume hierarchies
Spatial Data Structures
- Fundamental in computer science
- Other applications
- robotics, motion planning, simulation
- geographical information systems (GIS)
- sensor networks, routing, etc.
- In computer graphics:
- visibility, transparency rendering, physics-based animation & simulation, collision detection, morphing, geometric modeling, etc.
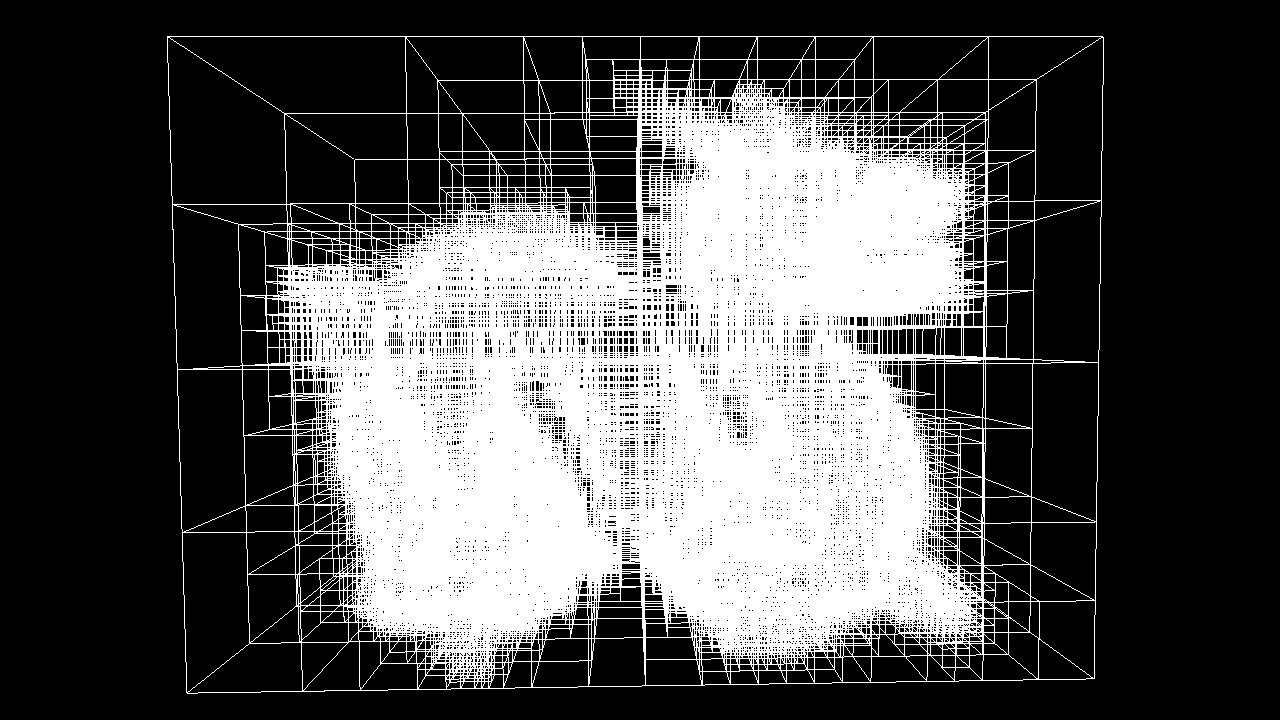
KD-Trees
- Construction
KD-Trees
- Construction
- compute bounding box
KD-Trees
- Construction
- compute bounding box
- recursively split cell using axis-aligned plane until maximum depth or minimum number of remaining objects is reached
- Only leaf nodes store reference to geometry!
KD-Trees
- Construction
- compute bounding box
- recursively split cell using axis-aligned plane until maximum depth or minimum number of remaining objects is reached
- Only leaf nodes store reference to geometry!
- choosing the split plane
- midpoint
- median cut
- advanced strategies
- builds a binary tree structure
KD-Trees
- Internal nodes store
- split axis: \(x\)-, \(y\)-, or \(z\)-axis
- split position: coordinate of split plane along axis
- children: reference to child nodes
- Leaf nodes store
- list of primitives
- mailboxing information
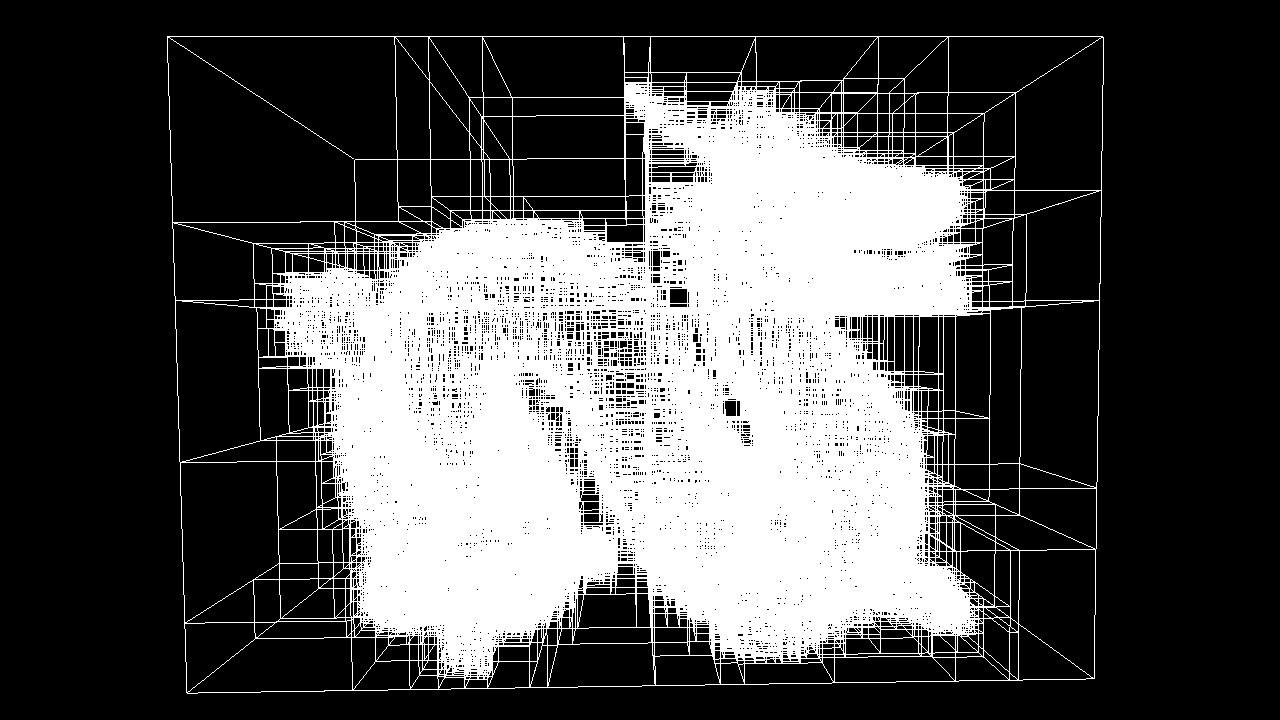
KD-Trees
- Traversal
- top-down recursion
KD-Trees
- Traversal
- top-down recursion
KD-Trees
- Traversal
- top-down recursion
KD-Trees
- Traversal
- top-down recursion
KD-Trees
- Traversal
- top-down recursion
KD-Trees
- Traversal
- top-down recursion
KD-Trees
KD-Trees
KD-Trees
Bounding Volume Hierarchies
- So far: divide space and assign objects to cells
- Now: group objects and bound by simple volumes for fast ray-intersection rejection
- Alternative divide-and-conquer method
Bounding Volume Hierarchies
- Bounding Volumes
- Spheres
Bounding Volume Hierarchies
- Bounding Volumes
- Spheres
- Axis-aligned bounding box (AABB)
Bounding Volume Hierarchies
- Bounding Volumes
- Spheres
- Axis-aligned bounding box (AABB)
- Oriented bounding box (OBB)
Bounding Volume Hierarchies
- Bounding Volumes
- Spheres
- Axis-aligned bounding box (AABB)
- Oriented bounding box (OBB)
- \(k\)-discrete orientation polytopes (\(k\)-DOPs)
- convex hulls, etc.
- Tradeoff
- complex shape → tight fit → fewer intersections
- simple shape → fast intersection
Bounding Volume Hierarchies
- Construction: bottom-up
Bounding Volume Hierarchies
- Traversal: recursive top-down
each geometric primitive intersected only once (no mailboxing required)
Comparison
- Spatial subdivision
- selects sets of objects based on given volumes
- top-down construction
- Bounding volume hierarchies
- selects volume based on given sets of objects
- bottom-up construction
Exploiting Hardware
- Caching
- Parallelism
- SIMD extensions
- Programmable GPUs
- Dedicated ray-tracing hardware
Summary
- Brute-Force
- Intersect ray with all \(n\) triangles of the mesh
- Select intersection with smallest positive ray parameter \(t\)
- Computational cost: \(\mathcal{O}(n)\)
- Bounding Volumes
- Bound mesh by simple-to-interesect objects (sphere, box, etc.)
- Only if ray intersects bounding volume, then test individual triangles
- Bounding volume hierarchy leads to \(\mathcal{O}(\log n)\)
- Spatial Hierarchy
- Partition scene into a spatial hierarchy
- Grid, Octree, kD-tree, BSP-tree
- Spatial hierarchy leads to \(\mathcal{O}(\log n)\)
Axis-Aligned Bounding Boxes
- AABBs are simple to code, but quite effective (see exercises)

Dynamic Scenes?
Photorealistic Rendering
The Quest for Realism
 standard ray tracing
standard ray tracing  +soft shadows
+soft shadows
 +caustics
+caustics  +indirect lighting
+indirect lighting
© Henrik Wann Jensen
Light Paths
- E = eye point
- L = light source
- D = diffuse reflection
- S = specular reflection
Types of Reflections

H. Lensch, “Efficient Image-Based Appearance Acquisition of Real-World Objects”, PhD thesis, 2004
Quiz: Light Paths
Which light paths can a standard recursive ray-tracer handle?
- \(ED^*L\)
- Nope, this is what a very different algorithm called Radiosity can handle. Wikipedia
- \(E[(D|G|S)^+(D|G)]L\)
- No, this is Kajiya’s path-tracing algorithm. Wikipedia
- \(E(D|G)[S^*]L\)
- No, after a diffuse bounce, we cannot trace further specular bounces!
- \(E[S^*](D|G)L\)
- Yes, we can handle light rays from the eye that first go through an arbitrary number of mirror reflections, then one diffuse/glossy bounce where the intersection point is connected to the light source using shadow rays (Phong lighting model). Note that multiple paths of different length can be combined in a single pixel.
- Notation:
- \(+\) = one or more occurrences
- \(*\) = zero or more occurrences
- \(()\) = grouping
- \(|\) = or
Recursive Ray Tracing
Which light paths can a standard recursive ray-tracer handle?
- Only \(E[S^*](D|G)L\)

- No multiple diffuse inter-reflections
- E.g. \(EDDL\)

- No caustics
- E.g. \(EDSL\)

Literature
- Botsch, Kobbelt, Pauly, Alliez, Levy: Polygon Mesh Processing, AK Peteres, 2010.
- Chapters 1.3 and 2

- Pharr, Humphreys: Physically Based Rendering, Morgan Kaufmann, 2004.
- Chapter 3

- Hughes et al.: Computer Graphics: Principles and Practice, 3rd Edition, Addison-Wesley, 2014.
- Chapters 25, 37


